题目内容
14.在正数范围内定义运算“*”,其规则为a*b=a+b2,则方程x*(x+1)=5的解是x=1.分析 根据新定义得到x+(x+1)2=5,整理得x2+3x-4=0,再利用因式分解法解方程得到x1=-4(舍去),x2=1,然后根据新定义的条件确定x的值.
解答 解:∵x*(x+1)=5,
∴x+(x+1)2=5,
整理得x2+3x-4=0,
(x+4)(x-1)=0,
所以x1=-4(舍去),x2=1,
即x=1
故答案为x=1.
点评 本题考查了解一元二次方程-因式分解法:就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
15.一个数减去2等于-3,则这个数是( )
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
9.为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费,如表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费=自来水销售费用+污水处理费用)
已知小王家2014年2月份用水20吨,交水费66元;3月份用水25吨,交水费91元.
(1)求a、b的值;
(2)随着夏天的到来用水量将增加,为了节约开支,小王计划把6月份水费控制在家庭月收入的2%,若小王家月收入为9200元,则小王家6月份最多能用水多少吨?
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
(1)求a、b的值;
(2)随着夏天的到来用水量将增加,为了节约开支,小王计划把6月份水费控制在家庭月收入的2%,若小王家月收入为9200元,则小王家6月份最多能用水多少吨?
6.先阅读下列一段文字,然后解答问题:
某食品研究部门欲将甲、乙、丙三种食物混合研制成100千克食物,并规定:研制成的混合食品中至少需含44000单位的维生素A和48000单位的维生素B,三种食物的维生素A、B的含量如表1所示:
(表1)(表2)
设所取甲、乙、丙三种食物的质量分别为x千克、y千克、z千克,
(1)试根据题意列出等式和不等式,并说明:①y≥20;②2x-y≥40;
(2)设甲、乙、丙三种食物的生产成本如表2所示:①试用含x、y的代数式表示研制的混合食品的总成本P(元);②如果限定混合食品中甲种食物的质量为40千克,试求此时总成本P的取值范围,并确定当P取最小值时,所取乙、丙两种食物的质量.
某食品研究部门欲将甲、乙、丙三种食物混合研制成100千克食物,并规定:研制成的混合食品中至少需含44000单位的维生素A和48000单位的维生素B,三种食物的维生素A、B的含量如表1所示:
| 甲种 食物 | 乙种 食物 | 丙种 食物 | 每千克生产成本(元) | |||
| 甲种食物 | 9 | |||||
| 维生素A(单位/千克) | 400 | 600 | 400 | 乙种食物 | 12 | |
| 维生素B(单位/千克) | 800 | 200 | 400 | 丙种食物 | 8 |
设所取甲、乙、丙三种食物的质量分别为x千克、y千克、z千克,
(1)试根据题意列出等式和不等式,并说明:①y≥20;②2x-y≥40;
(2)设甲、乙、丙三种食物的生产成本如表2所示:①试用含x、y的代数式表示研制的混合食品的总成本P(元);②如果限定混合食品中甲种食物的质量为40千克,试求此时总成本P的取值范围,并确定当P取最小值时,所取乙、丙两种食物的质量.
 如图,锐角△ABC是⊙O内接三角形,弦AE⊥BC,垂足为D.在AD上取点F,使FD=DE,连接CF,并延长交AB于点G.求证:CG⊥AB.
如图,锐角△ABC是⊙O内接三角形,弦AE⊥BC,垂足为D.在AD上取点F,使FD=DE,连接CF,并延长交AB于点G.求证:CG⊥AB.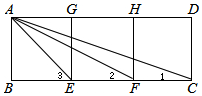 如图,四边形ABEG、GEFH、HFCD都是边长相等的正方形
如图,四边形ABEG、GEFH、HFCD都是边长相等的正方形