题目内容
2．写出5个数（不允许重复），同时满足下列4个条件：①有1个数既不是正数，也不是负数；
②其中3个不是负数；
③其中至少有1个是正分数；
④其中只有1个是负整数．
分析 根据题意可知有2个正数、2个负数、另一个为0，然后写出符合题意的5个有理数即可．
解答 解：根据题意可知有1个正整数、1个正分数，1个负整数，1个负整数、另一个为0，
故答案为：1，$\frac{1}{2}$，0，-1，-$\frac{1}{2}$．
点评 本题主要考查的是正数和负数、有理数的分类，掌握有理数的概念和分类是解题的关键．
练习册系列答案
相关题目
3．下列计算正确的是（ ）
| A． | a2+a3=a5 | B． | a6-a4=a2 | C． | x2•x3=x6 | D． | y3÷y=y2 |
4．若3＜m＜5，则$\sqrt{（3-m）^{2}}$-$\sqrt{（m-5）^{2}}$等于（ ）
| A． | -2 | B． | -2m+8 | C． | 2m-8 | D． | -2m+2 |
10．
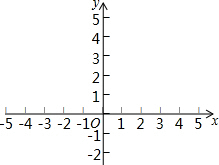问题：探究函数y=|x|-2的图象与性质．
小华根据学习函数的经验，对函数y=|x|-2的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）在函数y=|x|-2中，自变量x可以是任意实数；
（2）如表是y与x的几组对应值．
①m=1；
②若A（n，8），B（10，8）为该函数图象上不同的两点，则n=-10；
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；
根据函数图象可得：
①该函数的最小值为-2；
②已知直线${y_1}=\frac{1}{2}x-\frac{1}{2}$与函数y=|x|-2的图象交于C、D两点，当y1≥y时x的取值范围是-1≤x≤3．
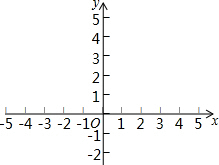问题：探究函数y=|x|-2的图象与性质．小华根据学习函数的经验，对函数y=|x|-2的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）在函数y=|x|-2中，自变量x可以是任意实数；
（2）如表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 1 | 0 | -1 | -2 | -1 | 0 | m | … |
②若A（n，8），B（10，8）为该函数图象上不同的两点，则n=-10；
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；
根据函数图象可得：
①该函数的最小值为-2；
②已知直线${y_1}=\frac{1}{2}x-\frac{1}{2}$与函数y=|x|-2的图象交于C、D两点，当y1≥y时x的取值范围是-1≤x≤3．
7．已知x与y之间的关系如表所示：
下面用x表示y的式子中，正确的是（ ）
| x | 1 | 2 | 3 | 4 | … |
| y | 0.6+3 | 0.6+6 | 0.6+9 | 0.6+12 | … |
| A． | y=0.6+x | B． | y=0.6+3x | C． | y=0.6×3+x | D． | y=0.6×3-x |
