题目内容
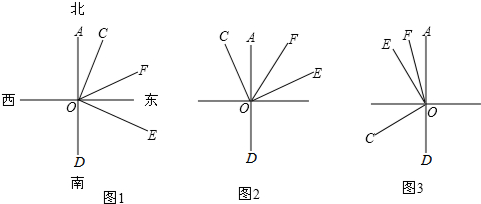
如图,0为直线AD上的一点,射线OA表示O点的正北方向,射线OC表示O点的北偏东m°方向,射线OE表示O点的南偏东n°的方向,射线OF平分∠AOE,且2m+2n=180.
(1)如图1,∠COE= °,∠COF和∠DOE之间的数量关系为 .
(2)若将∠COE绕点O旋转至图2的位置,请写出∠COF和∠DOE之间有何数量关系并说明理由;
(3)若将∠COE绕点0旋转至图3的位置,射线OF仍然平分∠AOE时,请写出∠COF和∠DOE之间有何数量关系并说明理由.
(1)如图1,∠COE=
(2)若将∠COE绕点O旋转至图2的位置,请写出∠COF和∠DOE之间有何数量关系并说明理由;
(3)若将∠COE绕点0旋转至图3的位置,射线OF仍然平分∠AOE时,请写出∠COF和∠DOE之间有何数量关系并说明理由.

考点:方向角,角的计算
专题:几何图形问题,探究型
分析:(1)根据方向角的定义,以及∠COE=180-m-n,即可求解;
(2)根据∠COF=90°-∠EOF,∠EOF=
∠AOE=
(180°-∠BOE)=
∠BOE即可证得;
(3)根据角的和差,以及角平分线的定义即可求解.
(2)根据∠COF=90°-∠EOF,∠EOF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据角的和差,以及角平分线的定义即可求解.
解答:解:(1)∵2m+2n=180
∴m+n=90
∠COE=180-m-n=90°,∠BOE=2∠COF;
(2)不发生变化.证明如下:
∵∠COE=90°
∴∠COF=90°-∠EOF
=90°-
∠AOE
=90°-
(180°-∠BOE)
=90°-90°+
∠BOE
=
∠BOE.
∴∠BOE=2∠COF
(3)∵∠COF=∠COE+∠EOF=90°+∠EOF,
∠DOE=∠COD+∠COE=90°+∠EOF,
∴∠DOE+∠COF=180°+2∠EOF,
又∵∠AOE=2∠EOF,
∴∠DOE+∠COF=180°+∠AOE,
∴∠DOE+2∠COF=360°.
∴m+n=90
∠COE=180-m-n=90°,∠BOE=2∠COF;
(2)不发生变化.证明如下:
∵∠COE=90°
∴∠COF=90°-∠EOF
=90°-
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
=90°-90°+
| 1 |
| 2 |
=
| 1 |
| 2 |
∴∠BOE=2∠COF
(3)∵∠COF=∠COE+∠EOF=90°+∠EOF,
∠DOE=∠COD+∠COE=90°+∠EOF,
∴∠DOE+∠COF=180°+2∠EOF,
又∵∠AOE=2∠EOF,
∴∠DOE+∠COF=180°+∠AOE,
∴∠DOE+2∠COF=360°.
点评:本题主要考查了方向角的定义,以及角平分线的定义,对定义的熟练掌握是解题关键.

练习册系列答案
相关题目
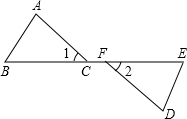 如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是
如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是
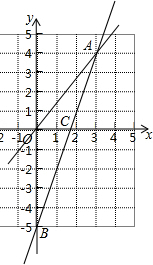 如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C.
如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C.