题目内容
已知两圆的半径长是方程x2-10x+24=0的两个解,且两圆的圆心距为d,若两圆相离,则下列结论正确的是( )
| A、0<d<2 |
| B、d>10 |
| C、0≤d<2或d>10 |
| D、0<d<2或d>10 |
考点:圆与圆的位置关系,解一元二次方程-因式分解法
专题:计算题
分析:首先解得方程求得两圆的半径,然后根据两圆相离分外离和内含两种情况分类讨论得到答案即可.
解答:解:∵两圆的半径长是方程x2-10x+24=0的两个解,
∴解得:x=4或x=6,
∴两圆的半径分别为∴4和6,
∵两圆相离,
∴当两圆外离时,d>R+r
即:d>10,
当两圆内含时,0≤d<R-r,
即:0≤d<2,
故选C.
∴解得:x=4或x=6,
∴两圆的半径分别为∴4和6,
∵两圆相离,
∴当两圆外离时,d>R+r
即:d>10,
当两圆内含时,0≤d<R-r,
即:0≤d<2,
故选C.
点评:本题考查了圆与圆的位置关系,解题中能分外离和内切讨论是解答本题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
若关于x的一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=-
,x1•x2=
.当a=1,b=6,c=5时,x1x2+x1+x2的值是( )
| b |
| a |
| c |
| a |
| A、5 | B、-5 | C、1 | D、-1 |
某工厂今年纯利润达到1200亿元,1200亿元用科学记数法表示为( )
| A、1.2×108元 |
| B、1.2×1010元 |
| C、1.2×1011元 |
| D、1.2×109元 |
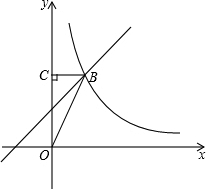 如图,一次函数y=x+b与反比例函数y=
如图,一次函数y=x+b与反比例函数y=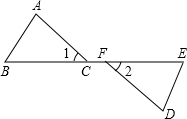 如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是
如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是