题目内容
学校沿路护栏纹饰部分设计成若干个相同的菱形图案,每增加一个菱形图案,纹饰长度就增加dcm,如图.已知每个菱形的横向对角线长为40cm.
(1)若该纹饰要221个菱形图案,试用含d的代数式表示纹饰的长度L;当d=30时,求该纹饰的长度L;
(2)当d=25时,若保持(1)中纹饰长度不变,则需要多少个这样的菱形图案?

(1)若该纹饰要221个菱形图案,试用含d的代数式表示纹饰的长度L;当d=30时,求该纹饰的长度L;
(2)当d=25时,若保持(1)中纹饰长度不变,则需要多少个这样的菱形图案?
考点:规律型:图形的变化类,列代数式,代数式求值
专题:几何变换
分析:(1)根据题意可知,第一个菱形横向对角线长为40cm,以后每增加一个就加dcm,根据共有221菱形图案,故增加的菱形图案为221-1,故增加的长度为(221-1)d,则L=40+(221-1)d,代入d=30时,可求该纹饰的长度L;
(2)保持(1)中纹饰长度不变,根据d的值求解.
(2)保持(1)中纹饰长度不变,根据d的值求解.
解答:解:(1)因为以后每增加一个就加dcm,
L=40+(221-1)d,
当d=30cm时,
L=40+(221-1)×30=6640(cm);
(2)当d=25时,
需要菱形图案的个数=
+1=265.
L=40+(221-1)d,
当d=30cm时,
L=40+(221-1)×30=6640(cm);
(2)当d=25时,
需要菱形图案的个数=
| 6640-40 |
| 25 |
点评:本题考查了图形变化类,关键是看到总长度和d的关系,以及第(2)问以长度相等作为等量关系.

练习册系列答案
相关题目
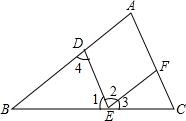 填空,完成下列说理过程.
填空,完成下列说理过程.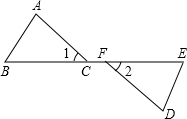 如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是
如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是
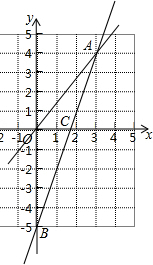 如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C.
如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C.