题目内容
13.如图,在△ABE中,AE=AB,以AB为直径的⊙O交AE于点D,交BE于点F,过点B的直线与AE的延长线相交于点C,且∠EBC=$\frac{1}{2}$∠BAC.(1)判断BC与⊙O有什么位置关系,并说明理由;
(2)过点E作EG垂直BC于点G,若AB=8,sin∠EBC=$\frac{1}{4}$,求EG的长;
(3)在满足第(2)问的前提下,求AC的长.
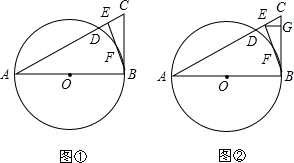
分析 (1)连接AF,由AB为⊙O的直径,得出∠AFB=90°,证△ABE为等腰三角形,得出∠BAF=$\frac{1}{2}$∠BAC,由∠EBC=$\frac{1}{2}$∠BAC,证出∠ABC=90°,BC⊥AB,即可得出BC与⊙O相切;
(2)先由三角函数求出BF,得出BE=2BF=4,即可求出EG;
(3)证明△CEG∽△CAB,得出比例式$\frac{CE}{CA}=\frac{EG}{AB}$,求出CE,即可得出AC=AE+CE=$\frac{64}{7}$.
解答 解:(1)BC与⊙O相切;理由如下:
连接AF,如图1所示: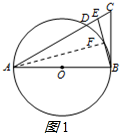 ∵AB为⊙O的直径,
∵AB为⊙O的直径,
∴∠AFB=90°,
∵AE=AB,
∴△ABE为等腰三角形,
∴∠BAF=$\frac{1}{2}$∠BAC,
∵∠EBC=$\frac{1}{2}$∠BAC,
∴∠BAF=∠EBC,
∴∠BAF+∠FBA=∠EBC+∠FBA=90°,
∴∠ABC=90°,
∴BC⊥AB,
∴BC与⊙O相切;
(2)如图2所示: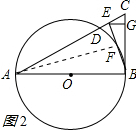 ∵∠BAF=∠EBC,
∵∠BAF=∠EBC,
∴sin∠BAF=sin∠EBC=$\frac{1}{4}$,
∴BF=AB•sin∠BAF=8×$\frac{1}{4}$=2,BE=2BF=4,
∴EG=BE•sin∠EBC=4×$\frac{1}{4}$=1;
(3)∵EG⊥BC,AB⊥BC,
∴EG∥AB,
∴△CEG∽△CAB,
∴$\frac{CE}{CA}=\frac{EG}{AB}$,
∴$\frac{CE}{CE+8}=\frac{1}{8}$,
∴CE=$\frac{8}{7}$,
∴AC=AE+CE=8+$\frac{8}{7}$=$\frac{64}{7}$.
点评 本题是圆的综合题,考查了切线的判定、等腰三角形的判定与性质、三角函数的运用以及相似三角形的判定与性质;本题难度较大,综合性强,需要通过运用三角函数和三角形相似才能得出结果.

 快捷英语周周练系列答案
快捷英语周周练系列答案 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠3=20°,则∠2的度数等于( )
如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠3=20°,则∠2的度数等于( )| A. | 40° | B. | 45° | C. | 50° | D. | 60° |
| A. | 54.32×104 | B. | 5.432×105 | C. | 5.432×106 | D. | 0.5432×106 |
| A. | a5 | B. | a6 | C. | a8 | D. | a9 |
 如图,二次函数y=ax2+bx+c的图象经过点(-1,0)、(3,0)和(0,2),当x=2时,y的值为2.
如图,二次函数y=ax2+bx+c的图象经过点(-1,0)、(3,0)和(0,2),当x=2时,y的值为2.