题目内容
2.已知关于x,y的方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=(3k-1)x+2}\end{array}\right.$,分别求出k,b为何值时,方程组:(1)有唯一解;
(2)有无数多个解;
(3)无解.
分析 先把①中y的值代入②,使方程变为只含x的一元一次方程,根据x的系数讨论方程组(1)有唯一一组解;(2)有无穷多组解;(3)无解时k,b的取值即可.
解答 解:把y=kx+b代入y=(3k-1)x+2中,
可得:(2k-1)x=b-2,
(1)当(2k-1)≠0,即k≠0.5,方程有唯一解x=$\frac{b-2}{2k-1}$,将此x的值代入y=kx+b中,
得:y=$\frac{3kb-2k-b}{2k-1}$,因而原方程组有唯一一组解;
(2)当(2k-1)=0且b-2=0时,即k=0.5,b=2时,方程有无穷多个解,因此原方程组有无穷多组解;
(3)当(2k-1)=0且(b-2)≠0时,即k=0.5,b≠2时,方程无解,因此原方程组无解.
点评 本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.

练习册系列答案
相关题目
7.地球绕太阳公转的速度约是110000千米/时,将110000用科学记数法表示为( )
| A. | 11×104 | B. | 1.1×104 | C. | 1.1×105 | D. | 0.11×106 |
12.-2的相反数的倒数是( )
| A. | 2 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
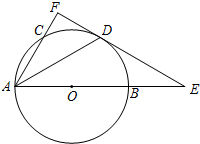 如图,AB是⊙O的直径,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
如图,AB是⊙O的直径,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.