题目内容
18. 如图,二次函数y=ax2+bx+c的图象经过点(-1,0)、(3,0)和(0,2),当x=2时,y的值为2.
如图,二次函数y=ax2+bx+c的图象经过点(-1,0)、(3,0)和(0,2),当x=2时,y的值为2.
分析 把三点坐标代入二次函数解析式求出a,b,c的值,即可确定出二次函数解析式,然后把x=2代入解析式即可求得.
解答 解:∵二次函数y=ax2+bx+c的图象经过点(-1,0)、(3,0)和(0,2),
∴$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{4}{3}}\\{c=2}\end{array}\right.$,
则这个二次函数的表达式为y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2.
把x=2代入得,y=-$\frac{2}{3}$×4+$\frac{4}{3}$×2+2=2.
故答案为2.
点评 此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若xmyn÷$\frac{1}{4}$x3y=4x2,则m,n的值分别是( )
| A. | m=6,n=1 | B. | m=5,n=1 | C. | m=5,n=0 | D. | m=6,n=0 |
7.地球绕太阳公转的速度约是110000千米/时,将110000用科学记数法表示为( )
| A. | 11×104 | B. | 1.1×104 | C. | 1.1×105 | D. | 0.11×106 |
8.用半径为5cm的扇形纸片卷成一个圆锥形的无底纸帽,纸帽的底面周长为4πcm,则此圆锥纸帽的面积等于( )
| A. | 10πcm2 | B. | 14πcm2 | C. | 20πcm2 | D. | 40πcm2 |
 如图,在边长为a的正方形ABCD中,分别以B,D分圆心,以a为半径在正方形内部画弧,形成了叶子形图案(阴影部分),则这个叶片形图案的周长为πa.
如图,在边长为a的正方形ABCD中,分别以B,D分圆心,以a为半径在正方形内部画弧,形成了叶子形图案(阴影部分),则这个叶片形图案的周长为πa.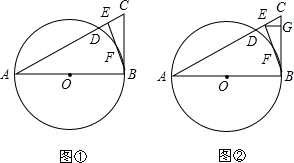
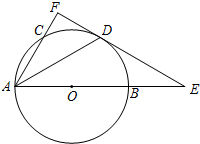 如图,AB是⊙O的直径,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
如图,AB是⊙O的直径,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.