题目内容
15.直线l:y=-$\frac{3}{4}$x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图象指出当m的函数值大于0的函数值时x的取值范围.分析 先根据函数的解析式求出A、B两点的坐标,再求出点C的坐标,利用待定系数法求出抛物线m的解析式,画出其图象,利用数形结合即可求解.
解答  解:∵y=-$\frac{3}{4}$x+6交y轴于点A,与x轴交于点B,
解:∵y=-$\frac{3}{4}$x+6交y轴于点A,与x轴交于点B,
∴x=0时,y=6,
∴A(0,6),
y=0时,x=8,
∴B(8,0),
∵过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),BC=5,
∴C(3,0).
设抛物线m的解析式为y=a(x-3)(x-8),
将A(0,6)代入,得24a=6,解得a=$\frac{1}{4}$,
∴抛物线m的解析式为y=$\frac{1}{4}$(x-3)(x-8),即y=$\frac{1}{4}$x2-$\frac{11}{4}$x+6;
函数图象如右:
当抛物线m的函数值大于0时,x的取值范围是x<3或x>8.
点评 本题考查了二次函数与不等式,待定系数法求二次函数的解析式,一次函数图象上点的坐标特征,正确求出二次函数的解析式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.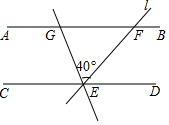 如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=80°,那么∠GFE=( )
如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=80°,那么∠GFE=( )
 如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=80°,那么∠GFE=( )
如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=80°,那么∠GFE=( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
20.如果把一个锐角△ABC的三边的长都扩大为原来的3倍,那么锐角A的余切值( )
| A. | 扩大为原来的3倍 | B. | 缩小为原来的$\frac{1}{3}$ | C. | 没有变化 | D. | 不能确定 |
 如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则矩形ABCD的面积为16$\sqrt{3}$cm2.
如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则矩形ABCD的面积为16$\sqrt{3}$cm2. 如图,D为△ABC的边AB上一点,如果∠ACD=∠ABC时,那么图中AC是AD和AB的比例中项.
如图,D为△ABC的边AB上一点,如果∠ACD=∠ABC时,那么图中AC是AD和AB的比例中项.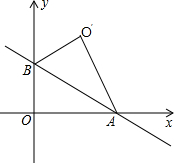 如图,直线y=-$\frac{\sqrt{3}}{3}$x+2与x轴、y轴分别交于A、B两点,把△AOB沿直线AB翻折后得到△AO′B,则点O′的坐标是($\sqrt{3}$,3).
如图,直线y=-$\frac{\sqrt{3}}{3}$x+2与x轴、y轴分别交于A、B两点,把△AOB沿直线AB翻折后得到△AO′B,则点O′的坐标是($\sqrt{3}$,3).