题目内容
3. 如图,D为△ABC的边AB上一点,如果∠ACD=∠ABC时,那么图中AC是AD和AB的比例中项.
如图,D为△ABC的边AB上一点,如果∠ACD=∠ABC时,那么图中AC是AD和AB的比例中项.
分析 根据两角分别相等的两个三角形相似,可得△ACD∽△ABC的关系,根据相似三角形的性质,可得答案.
解答 解:在△ACD与△ABC中,
∠ACD=∠ABC,∠A=∠A,
∴△ACD∽△ABC,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,
∴AC是AD和AB的比例中项.
故答案为AC.
点评 本题考查了相似三角形的判定与性质,比例线段,得出△ACD∽△ABC是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
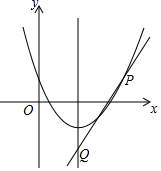 如图,抛物线y=ax2-(2a+1)x+b的图象经过(2,-1)和(-2,7)且与直线y=kx-2k-3相交于点P(m,2m-7).
如图,抛物线y=ax2-(2a+1)x+b的图象经过(2,-1)和(-2,7)且与直线y=kx-2k-3相交于点P(m,2m-7).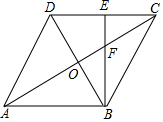 已知:如图,菱形ABCD,对角线AC、BD交于点O,BE⊥DC,垂足为点E,交AC于点F.求证:
已知:如图,菱形ABCD,对角线AC、BD交于点O,BE⊥DC,垂足为点E,交AC于点F.求证: