题目内容
15.下列等式成立的是( )| A. | $\frac{a}{b}$=$\frac{{a}^{2}}{{b}^{2}}$ | B. | $\frac{a}{b}$=$\frac{a+c}{b+c}$ | C. | $\frac{a}{b}$=$\frac{a-c}{b-c}$ | D. | $\frac{a}{b}$=$\frac{ma}{mb}$(m≠0) |
分析 根据分式的分子分母都乘以(或除以)同一个不为零数(或整式),分式的值不变,可得答案.
解答 解:A、分式的乘方,分式的值发生变化,故A错误;
B、分式的分子分母都加同一个整式,分式的值发生变化,故B错误;
C、分式的分子分母都减同一个整式,分式的值发生变化,故C错误;
D、分式的分子分母都乘以(或除以)同一个不为零数(或整式),分式的值不变,故D正确;
故选:D.
点评 本题考查了分式的基本性质,分式的分子分母都乘以(或除以)同一个不为零数(或整式),分式的值不变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.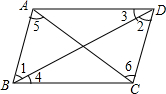 如图,若∠3=∠4,则下列结论:①AB∥CD;②AD∥BC;③∠1=∠2;④∠5=∠6,其中正确的有( )
如图,若∠3=∠4,则下列结论:①AB∥CD;②AD∥BC;③∠1=∠2;④∠5=∠6,其中正确的有( )
 如图,若∠3=∠4,则下列结论:①AB∥CD;②AD∥BC;③∠1=∠2;④∠5=∠6,其中正确的有( )
如图,若∠3=∠4,则下列结论:①AB∥CD;②AD∥BC;③∠1=∠2;④∠5=∠6,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.受中日钓鱼岛事件的影响,在钓鱼岛被“国有化”的2012年9月份,某日本品牌食用油价格开始回落,食用油批发商批发这种品牌的食用油,每桶在9月份前四周每周的平均销售价格变化如下表:
进入10月份后,由于受中日关系趋于缓和等因素的影响,食用油的价格开始回升,该品牌食用油销售价格y2(元/桶)从10月份第1周的54元/桶,上升至第2周的57元/桶,且销售价格y2(元/桶)与周数x(x为整数)的变化情况满足二次函数:y2=-$\frac{1}{4}$x2+bx+c.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出9月份y1与x的函数关系式;并求出10月份y2与x的函数关系式.
(2)若9月份该品牌的食用油进价m1(元/桶)与周数x满足函数关系为:m1=$\frac{1}{3}$x2-3x+50,10月份该品牌的食用油进价m2(元/桶)与周数x满足函数关系为:m2=$\frac{7}{2}$x+$\frac{81}{2}$,试问在9月份和10月份中,哪月的哪一周销售一桶该品牌的食用油利润最大?最大利润是多少?
(3)在第(2)问的条件下,该批发商在10月份的第2周以该周的进价购入该品牌食用油1200桶,准备在10月份第3周进行销售.在第3周以该周的销售价销售了a%后,为了加快销售的进度,该批发商决定在原销售价格的基础上每桶降价4元进行销售,这样顺利地完成了第三周销售1200桶的任务,且获利12000元,算出a的值.
| 周数x | 1 | 2 | 3 | 4 |
| 价格y1(元/桶) | 60 | 59 | 58 | 57 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出9月份y1与x的函数关系式;并求出10月份y2与x的函数关系式.
(2)若9月份该品牌的食用油进价m1(元/桶)与周数x满足函数关系为:m1=$\frac{1}{3}$x2-3x+50,10月份该品牌的食用油进价m2(元/桶)与周数x满足函数关系为:m2=$\frac{7}{2}$x+$\frac{81}{2}$,试问在9月份和10月份中,哪月的哪一周销售一桶该品牌的食用油利润最大?最大利润是多少?
(3)在第(2)问的条件下,该批发商在10月份的第2周以该周的进价购入该品牌食用油1200桶,准备在10月份第3周进行销售.在第3周以该周的销售价销售了a%后,为了加快销售的进度,该批发商决定在原销售价格的基础上每桶降价4元进行销售,这样顺利地完成了第三周销售1200桶的任务,且获利12000元,算出a的值.
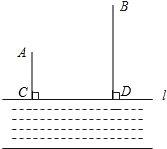 如图,A,B两个小镇在河流CD的同侧,到河的距离分别为AC=6千米,BD=14千米,且CD=15千米,现要在河边建一自来水厂,同时向A,B两镇供水,铺设水管的费用为每千米3万元,请你在河流CD上选择水厂的位置M,使铺设水管的费用最省,并求出总费用是多少?
如图,A,B两个小镇在河流CD的同侧,到河的距离分别为AC=6千米,BD=14千米,且CD=15千米,现要在河边建一自来水厂,同时向A,B两镇供水,铺设水管的费用为每千米3万元,请你在河流CD上选择水厂的位置M,使铺设水管的费用最省,并求出总费用是多少? 已知如图,∠A=60°,∠B=50°,CD平分∠BCE,则∠BCD=55°.
已知如图,∠A=60°,∠B=50°,CD平分∠BCE,则∠BCD=55°. 在△ABC中,DE∥BC交AB于D,交AC于E,且AD:DB=2:3,△ABC的周长为27cm,求△ADE的周长.
在△ABC中,DE∥BC交AB于D,交AC于E,且AD:DB=2:3,△ABC的周长为27cm,求△ADE的周长.