Question

3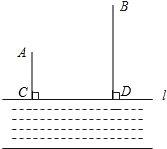．如图，A，B两个小镇在河流CD的同侧，到河的距离分别为AC=6千米，BD=14千米，且CD=15千米，现要在河边建一自来水厂，同时向A，B两镇供水，铺设水管的费用为每千米3万元，请你在河流CD上选择水厂的位置M，使铺设水管的费用最省，并求出总费用是多少？

Answer 1

分析 根据题意，要使铺设水管的费用最省，则自来水厂与A、B两个小镇的距离和最小，所以作出点A关于直线l的对称点A′，连接BA′，则BA′与直线l的交点即是水厂的位置M，根据勾股定理，求出A′B的长度，再根据总价=单价×数量，即可得出答案．

解答 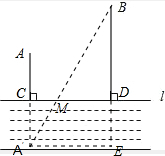解：作点A关于直线CD的对称点A'．连接BA'，交CD于点M，则A'B=AM+BM，
此时AM+BM为铺设水管的最短路线，
过A'作CD的平行线，交BD的延长线于点E，得Rt△A'BE，
∵DE=A'C=AC=6千米，BE=DE+BD=20千米，A'E=CD=15千米，∴A'B=$\sqrt{{{A}^{′}E}^{2}+E{B}^{2}}$=$\sqrt{1{5}^{2}+2{0}^{2}}$=25，
∴总费用是：3×25=75（万元）．

点评 此题主要考查了轴对称-最短路线问题，用到的知识点是：直角三角形的性质、勾股定理的应用、总价=单价×数量，解答此题的关键是要明确：凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合所学轴对称变换来解决，多数情况要作点关于某直线的对称点．