题目内容
20．
已知如图，∠A=60°，∠B=50°，CD平分∠BCE，则∠BCD=55°．
分析 根据三角形外角的性质得到∠BCE=∠A+∠B=110°，然后根据角平分线的性质即可得到结论．
解答 解：∵∠A=60°，∠B=50°，
∴∠BCE=∠A+∠B=110°，
∵CD平分∠BCE，
∴∠BCD=$\frac{1}{2}$∠BCE=55°，
故答案为：55°．
点评 本题考查了三角形的外角的性质，角平分线的定义，熟练掌握三角形外角的性质是解题的关键．
练习册系列答案
全能测控一本好卷系列答案
相关题目
如图，四边形PMNQ是正方形，△ABC的高AD=6cm，BC=12cm，则正方形PMNQ的边长是4cm．
15．下列等式成立的是（ ）
| A． | $\frac{a}{b}$=$\frac{{a}^{2}}{{b}^{2}}$ | B． | $\frac{a}{b}$=$\frac{a+c}{b+c}$ | C． | $\frac{a}{b}$=$\frac{a-c}{b-c}$ | D． | $\frac{a}{b}$=$\frac{ma}{mb}$（m≠0） |
9．
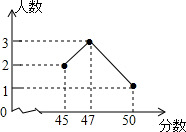在2015年的体育中考中，某校6名学生的体育成绩统计如图，则这组数据的众数、中位数分别是（ ）
在2015年的体育中考中，某校6名学生的体育成绩统计如图，则这组数据的众数、中位数分别是（ ）| A． | 3，2.5 | B． | 47，46 | C． | 47，47 | D． | 50，47 |
如图，是某油田的四口油井的位置图，图中1cm表示实际距离1.5km．请你仔细观察，并量一量图中的距离，用语言叙述这四口油井之间的位置关系．