题目内容
如图，?ABCD的对角线AC和BD相交于点E，AC=24，BD=38，AD=28，则△ADE的周长是（ ）| A、59 | B、56 | C、51 | D、45 |
考点：平行四边形的性质
专题：
分析：根据平行四边形的对角线互相平分，可得AE、DE的长度，继而可得△ADE的周长．
解答：解：∵四边形ABCD是平行四边形，
∴AE=CE=
AC=12，BE=DE=
BD=19，
∴△ADE的周长=AE+DE+AD=59．
故选：A．
∴AE=CE=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ADE的周长=AE+DE+AD=59．
故选：A．
点评：本题考查了平行四边形的性质，解答本题的关键是掌握平行四边形的对角线互相平分．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
如图，在直角梯形ABCD中，∠ABC=90°，AD∥BC，AD=6，AB=8，BC=9，点P是AB上一个动点，当PC+PD的和最小时，PB的长为
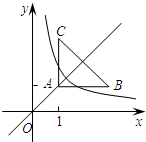如图，等腰直角三角形ABC位于第一象限，AB=AC=2，直角顶点A在正比例函数y=x的图象上，其中A点的横坐标为1，且两条直角边AB、AC分别平行于x轴、y轴，若函数y=| k |
| x |
| A、1＜k＜2 |
| B、1≤k≤3 |
| C、1≤k≤4 |
| D、1≤k＜4 |
三角形两边之和为8，第三边上的高为2，面积大于5，第三边的范围是（ ）
| A、2＜a＜8 | B、5＜a＜8 |
| C、2＜a＜5 | D、不能确定 |
一个盒子里有完全相同的三个小球，球上分别标有数字-2，1，4．随机摸出一个小球（不放回），其数字为p，再随机摸出另一个小球其数字记为q，则满足关于x的方程x2+px+q=0有实数根的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
比较2
，3
，4
的大小，正确的是（ ）
| 5 |
| 3 |
| 2 |
A、2
| ||||||
B、3
| ||||||
C、2
| ||||||
D、4
|
