题目内容
5.在平面直角坐标系xOy中,已知一次函数的图象经过点(2,3)与(-3,-7).(1)求这个一次函数的解析式;
(2)求这个一次函数的图象与x轴、y轴的交点坐标.
分析 (1)设一次函数解析式为y=kx+b,把一次函数图象上两个已知点的坐标代入得到$\left\{\begin{array}{l}{2k+b=3}\\{-3k+b=-7}\end{array}\right.$,然后解方程组求出k、b即可得到一次函数解析式;
(2)分别计算出一次函数的函数值为0对应的自变量的值和自变量为0时所对应的函数值即可这个一次函数的图象与x轴、y轴的交点坐标.
解答 解:(1)设一次函数解析式为y=kx+b,
把(2,3),(-3,-7)代入得$\left\{\begin{array}{l}{2k+b=3}\\{-3k+b=-7}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$,
所以一次函数解析式为y=2x-1;
(2)当y=0时,2x-1=0,解得x=$\frac{1}{2}$,
所以一次函数与x轴的交点坐标为($\frac{1}{2}$,0);
当x=0时,y=2x-1=-1,
所以一次函数与y轴的交点坐标为(0,-1).
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b,再将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;然后解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
相关题目
15.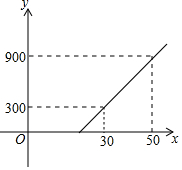 某旅客携带x(公斤)的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李质量x(公斤)的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李质量x(公斤)的对应关系,
某旅客携带x(公斤)的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李质量x(公斤)的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李质量x(公斤)的对应关系,
(1)如果旅客选择托运,求可携带的免费行李的最大质量为多少公斤?
(2)如果旅客选择快递,当1≤x≤15时,求快递费y2(元)与行李质量x(公斤)的函数关系式;
(3)某旅客携带25公斤的行李,设托运m(公斤)行李(10≤m<24,m为正整数),剩下的行李选择快递,m为何值时,总费用y的值最小,总费用的最小值是多少?
 某旅客携带x(公斤)的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李质量x(公斤)的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李质量x(公斤)的对应关系,
某旅客携带x(公斤)的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李质量x(公斤)的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李质量x(公斤)的对应关系,| 行李的质量x(公斤) | 快递费 |
| 不超过1公斤 | 10元 |
| 超过1公斤但不超过5公斤的部分 | 3元/公斤 |
| 超过5公斤但不超过15公斤的部分 | 5元/公斤 |
(2)如果旅客选择快递,当1≤x≤15时,求快递费y2(元)与行李质量x(公斤)的函数关系式;
(3)某旅客携带25公斤的行李,设托运m(公斤)行李(10≤m<24,m为正整数),剩下的行李选择快递,m为何值时,总费用y的值最小,总费用的最小值是多少?
10.某酒厂生产A,B两种品牌的酒,平均每天两种酒共可售出600瓶,每种酒每瓶的成本和售价如表所示,设平均每天共获利y元,平均每天售出A种品牌的酒x瓶.
(1)请写出y关于x的函数关系式;
(2)如果该厂每天至少投入成本25000元,且售出的B种品牌的酒不少于全天销售总量的55%,那么共有几种销售方案?并求出每天至少获利多少元?
| A | B | |
| 成本(元) | 50 | 35 |
| 售价(元) | 70 | 50 |
(2)如果该厂每天至少投入成本25000元,且售出的B种品牌的酒不少于全天销售总量的55%,那么共有几种销售方案?并求出每天至少获利多少元?
2.已知甲数的4倍比乙数的2倍大10,乙数的$\frac{1}{3}$比甲数少一半,则甲数是( )
| A. | 15 | B. | 10 | C. | 15或10 | D. | 以上都不是 |
 一只不透明的袋子中装有2个白球和一个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,小明想用树状图方法列出所有可能的结果,他正确地画出了第一次摸球的结果.
一只不透明的袋子中装有2个白球和一个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,小明想用树状图方法列出所有可能的结果,他正确地画出了第一次摸球的结果. 如图所示,把长方形ABCD沿EF折叠,若∠1=48°,则∠AEF等于114°.
如图所示,把长方形ABCD沿EF折叠,若∠1=48°,则∠AEF等于114°. 如图,在△ABC中,∠B=∠C,AE平分外角∠CAD.求证:AE∥BC.
如图,在△ABC中,∠B=∠C,AE平分外角∠CAD.求证:AE∥BC.