题目内容
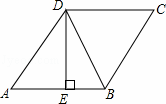
如图,在菱形ABCD中,DE⊥AB于点E,cosA=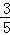 ,BE=4,则tan∠DBE的值是 .
,BE=4,则tan∠DBE的值是 .
2
考点: 菱形的性质;解直角三角形.
分析: 求出AD=AB,设AD=AB=5x,AE=3x,则5x﹣3x=4,求出x,得出AD=10,AE=6,在Rt△ADE中,由勾股定理求出DE=8,在Rt△BDE中得出tan∠DBE=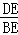 ,代入求出即可,
,代入求出即可,
解答: 解:∵四边形ABCD是菱形,
∴AD=AB,
∵cosA=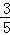 ,BE=4,DE⊥AB,
,BE=4,DE⊥AB,
∴设AD=AB=5x,AE=3x,
则5x﹣3x=4,
x=2,
即AD=10,AE=6,
在Rt△ADE中,由勾股定理得:DE=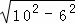 =8,
=8,
在Rt△BDE中,tan∠DBE= =
=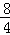 =2,
=2,
故答案为:2.
点评: 本题考查了菱形的性质,勾股定理,解直角三角形的应用,关键是求出DE的长.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
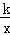 (k≠0)的图象经过点P(﹣2,3),则该函数的图象
(k≠0)的图象经过点P(﹣2,3),则该函数的图象
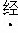
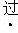 的点是( )
的点是( ) =
=  先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( )
先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( ) B.
B. 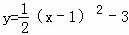 C.
C.  D.
D.