题目内容
.设a、b是常数,且b>0,抛物线y=ax2+bx+a2﹣5a﹣6为下图中四个图象之一,则a的值为( )
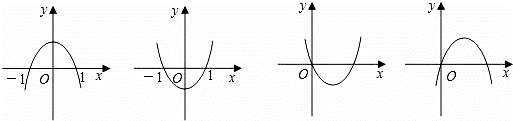
A. 6或﹣1 B. ﹣6或1 C. 6 D. ﹣1
D
考点: 二次函数的图象.
专题: 压轴题.
分析: 由b>0,排除前两个图象,第三个图象a>0,﹣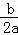 >0,推出b<0,与已知矛盾排除,从而抛物线y=ax2+bx+a2﹣5a﹣6的图象是第四个图,再求a的值.
>0,推出b<0,与已知矛盾排除,从而抛物线y=ax2+bx+a2﹣5a﹣6的图象是第四个图,再求a的值.
解答: 解:∵图1和图2表示y=0时,有1和﹣1两个根,代入方程能得出b=﹣b,即b=0,不合题意,
∴排除前两个图象;
∵第三个图象a>0,又﹣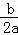 >0,
>0,
∴b<0,与已知矛盾排除,
∴抛物线y=ax2+bx+a2﹣5a﹣6的图象是第四个图,
由图象可知,抛物线经过原点(0,0),
∴a2﹣5a﹣6=0,解得a=﹣1或6,
∵a<0,∴a=﹣1.
故选D.
点评: 主要考查了从图象上把握有用的条件,准确选择数量关系解得a的值,简单的图象最少能反映出2个条件:开口方向,经过原点,利用这两个条件即可求出a的值.

练习册系列答案
相关题目
 S△BCD?若存在,求出此时t的值;若不存在,说明理由;
S△BCD?若存在,求出此时t的值;若不存在,说明理由;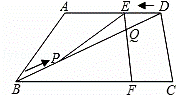
 ,b=﹣1.
,b=﹣1.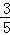 ,BE=4,则tan∠DBE的值是 .
,BE=4,则tan∠DBE的值是 .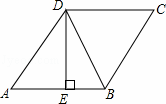

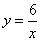 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第二象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第二象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线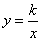 上运动,则
上运动,则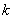 的值是 .
的值是 .
