题目内容
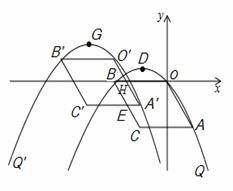
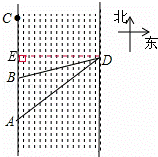
如图,美丽的徒骇河宛如一条玉带穿城而过,沿河两岸的滨河大道和风景带成为我市的一道新景观.在数学课外实践活动中,小亮在河西岸滨河大道一段AC上的A,B两点处,利用测角仪分别对东岸的观景台D进行了测量,分别测得∠DAC=60°,∠DBC=75°.又已知AB=100米,求观景台D到徒骇河西岸AC的距离约为多少米(精确到1米).(tan60°≈1.73,tan75°≈3.73)
考点: 解直角三角形的应用.
专题: 几何图形问题;数形结合.
分析: 如图,过点D作DE⊥AC于点E.通过解Rt△EAD和Rt△EBD分别求得AE、BE的长度,然后根据图示知:AB=AE﹣BE=100,把相关线段的长度代入列出关于ED的方程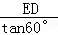 ﹣
﹣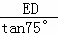 =100.通过解该方程求得ED的长度.
=100.通过解该方程求得ED的长度.
解答: 解:如图,过点D作DE⊥AC于点E.
∵在Rt△EAD中,∠DAE=60°,
∴tan60°=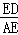 ,
,
∴AE=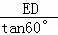
同理,在Rt△EBD中,
得到EB=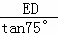 .
.
又∵AB=100米,
∴AE﹣EB=100米,
即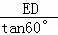 ﹣
﹣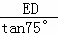 =100.
=100.
则ED=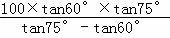 ≈
≈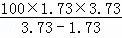 ≈323(米).
≈323(米).
答:观景台D到徒骇河西岸AC的距离约为323米.
点评: 本题考查了解直角三角形的应用.主要是正切概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
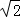 cm C. 5πcm D. 5
cm C. 5πcm D. 5 )÷(﹣1
)÷(﹣1 )+(﹣2)2×(﹣3)
)+(﹣2)2×(﹣3) +3
+3 B.
B.  C.
C.  D. 1﹣
D. 1﹣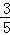 ,BE=4,则tan∠DBE的值是 .
,BE=4,则tan∠DBE的值是 .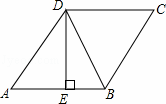

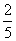 B.
B.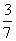 C.
C.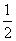 D.
D.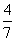
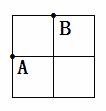
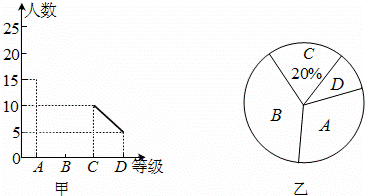
 单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平
单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平