题目内容


如图，王老师在上多边形外角和这节课时，做了一个活动，让小明在操场上从A点出发前进1m，向右转30°，再前进1m，又向右转30°，…，这样一直走下去，直到他第一次回到出发点A为止，他所走的路径构成了一个多边形．小明一共走了　　m，这个多边形的内角和是　          　度．


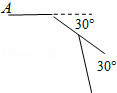
12     1800

考点： 多边形内角与外角． 

分析： 第一次回到出发点A时，所经过的路线正好构成一个外角是30度的正多边形，求得边数，即可求解．

解答： 解：∵所经过的路线正好构成一个外角是30度的正多边形，

∴360÷30=12，12×1=12m，

（12﹣2）×180°=1800°．

故答案为：12，1800．

点评： 本题考查了正多边形的外角的计算以及多边形的内角和，第一次回到出发点A时，所经过的路线正好构成一个外角是30度的正多边形是关键．

　


练习册系列答案
相关题目

如图，在菱形ABCD中，DE⊥AB于点E，cosA=，BE=4，则tan∠DBE的值是　 　．

如图，将△ABC绕点A按顺时针方向旋转某个角度得到△APQ，使AP平行于CB，CB，AQ的延长线相交于点D．如果∠D=40°，则∠BAC的度数为（　　）

　 A． 30° B． 40° C． 50° D． 60°

已知矩形ABCD中，AB=10cm，AD=4cm，作如下折叠操作．如图1和图2所示，在边AB上取点M，在边AD或边DC上取点P．连接MP．将△AMP或四边形AMPD沿着直线MP折叠得到△A′MP或四边形A′MPD′，点A的落点为点A′，点D的落点为点D′．

探究：

（1）如图1，若AM=8cm，点P在AD上，点A′落在DC上，则∠MA′C的度数为　 　；

（2）如图2，若AM=5cm，点P在DC上，点A′落在DC上，

①求证：△MA′P是等腰三角形；

②直接写出线段DP的长．

（3）若点M固定为AB中点，点P由A开始，沿A﹣D﹣C方向．在AD，DC边上运动．设点P的运动速度为1cm/s，运动时间为ts，按操作要求折叠．

①求：当MA′与线段DC有交点时，t的取值范围；

②直接写出当点A′到边AB的距离最大时，t的值；

发现：

若点M在线段AB上移动，点P仍为线段AD或DC上的任意点．随着点M位置的不同．按操作要求折叠后．点A的落点A′的位置会出现以下三种不同的情况：

不会落在线段DC上，只有一次落在线段DC上，会有两次落在线段DC上．

请直接写出点A′由两次落在线段DC上时，AM的取值范围是　 　．

如图，小正方形边长为1，连接小正方形的三个顶点，可得△ABC，则△ABC的面积是（　　）

　 A． 1 B． 1.5 C． 2 D． 2.5

“中国梦”是中华民族每一个人的梦，也是每一个中小学生的梦，各中小学开展经典诵读活动，无疑是“中国梦”教育这一宏大乐章里的响亮音符，学校在经典诵读活动中，对全校学生用A、B、C、D四个等级进行评价，现从中抽取若干个学生进行调查，绘制出了两幅不完整的统计图，请你根据图中信息解答下列问题：

（1）共抽取了多少个学生进行调查？

（2）将图甲中的折线统计图补充完整．

（3）求出图乙中B等级所占圆心角的度数．

如图①，将一张直角△ABC纸片折叠，使点A与点C重合，这时DE为折痕，△ECB为等腰三角形；继续将纸片沿△ECB的对称轴EF折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样的矩形为“叠加矩形”．

（1）如图②，正方形网格中的△ABC能折叠成“叠加矩形”吗？如果能，请在图②中画出折痕．

（2）如图③在正方形网格中，以给定的BC为一边，画出一个斜三角形△ABC，使其顶点A在格点上，且△ABC折成的“叠加矩形”为正方形．

（3）若一个三角形所折成的“叠加矩形”为正方形，那么必须满足的条件是什么？

（4）如果一个四边形一定能折成“叠加矩形”，那么它必须满足的条件是什么？

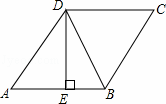
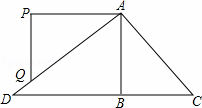
先化简，再求值：（+2﹣x）÷，其中x满足x2﹣4x+3=0．

 如图，已知BD，CD分别是∠ABC和∠ACE的角平分线，若∠A=45°，则∠D的度数      是（   ）

A.20                                 B.22.5         

C.25                                D.30                       

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网