��Ŀ����
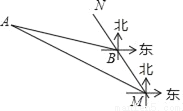
��ͼ��MN��ʾij��ˮ���̵�һ�����·�ߣ��ӵ�M����N������Ϊ��ƫ��30�㣬�ڵ�M�ı�ƫ��60�㷽������һ��A���Ե�AΪԲ�ģ���500��Ϊ�뾶��Բ������Ϊ��������ȡMN����һ��B�����BA�ķ���Ϊ��ƫ��75�㣮��֪MB=400�ף������ı䷽������ˮ·���Ƿ�ᴩ������������ͨ������˵�����ɣ����ο����ݣ�  ��1.732��
��1.732��
 ���ᴩ�������������ɼ�����.
�����������������Ҫ�ж���ˮ·���Ƿ�ᴩ������������Ҫ�Ƚϵ�A��MN�ľ�����500�Ĵ�С��Ҫ���A��MN�ľ��룬��AD��MN��MN�ڵ�D����AD=x�����ѱ�ʾ��DM=x+400������tan��AMD==�г����̣����x���Ƚ�x��500�Ĵ�С����x��500���ᴩ������������x��500����ᴩ��������.
���������
��������
��A��AD��MN�ڵ�D��...
���ᴩ�������������ɼ�����.
�����������������Ҫ�ж���ˮ·���Ƿ�ᴩ������������Ҫ�Ƚϵ�A��MN�ľ�����500�Ĵ�С��Ҫ���A��MN�ľ��룬��AD��MN��MN�ڵ�D����AD=x�����ѱ�ʾ��DM=x+400������tan��AMD==�г����̣����x���Ƚ�x��500�Ĵ�С����x��500���ᴩ������������x��500����ᴩ��������.
���������
��������
��A��AD��MN�ڵ�D��...
��֪����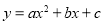 ��ͼ����ͼ��ʾ����ô����x�ķ���
��ͼ����ͼ��ʾ����ô����x�ķ��� �ĸ�������ǣ� ��
�ĸ�������ǣ� ��

A����ʵ����
B�����������ʵ����
C�����������ʵ��
D��������ͬ�Ų���ʵ����
 D��
��������
����������ߵ�ͼ����x�����������㣬����������������ǩ�3���߷��̣���ʱ������y=��2��x��ֵ����ͼ���֪��������ͬ�Ų���ʵ��������ѡD��
D��
��������
����������ߵ�ͼ����x�����������㣬����������������ǩ�3���߷��̣���ʱ������y=��2��x��ֵ����ͼ���֪��������ͬ�Ų���ʵ��������ѡD�� ������������һ����50�㣬����һ�����ϵĸ���ױߵļн��ǣ� ��
A. 25�� B. 40�� C. 25���40�� D. 50��
 C
���������ߵ�����������һ����50��
�������ֿ���
����������Ϊ50�㡢50�㡢80�㣻����������Ϊ50�㡢65�㡢65������˵�����£�
�ٵ�������Ϊ50�㡢50�㡢80��ʱ������ͼ�٣��ɵ���һ�����ϵĸ���ױߵļнǡ�DAB=40�㣻
�ڵ�������Ϊ50�㡢65�㡢65�㣬����ͼ�ڣ��ɵ���һ�����ϵĸ���ױߵļнǡ�DAB=25��ʹ�ѡ��C
�� ��
C
���������ߵ�����������һ����50��
�������ֿ���
����������Ϊ50�㡢50�㡢80�㣻����������Ϊ50�㡢65�㡢65������˵�����£�
�ٵ�������Ϊ50�㡢50�㡢80��ʱ������ͼ�٣��ɵ���һ�����ϵĸ���ױߵļнǡ�DAB=40�㣻
�ڵ�������Ϊ50�㡢65�㡢65�㣬����ͼ�ڣ��ɵ���һ�����ϵĸ���ױߵļнǡ�DAB=25��ʹ�ѡ��C
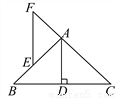
�� �� ��ͼ���ڡ�ABC�У�AB��AC��AD��BC��D��E��AB�ϵ�һ�㣬EF��AD��CA���ӳ�����F.
��֤����AEF�ǵ��������Σ�
 ������
��������������������ȸ��ݵ��������εױ��ϵ����ߺ�һ�����ɵã�ADΪ��BAC�Ľ�ƽ���ߣ�����ƽ���ߵ����ʵó���F=��CAD����FEA=��BAD���Ӷ���FEA=��F���ó����������Σ�
�����������AB=AC��AD��BC�� ���BAD=��CAD�� �֡�AD��EF��
���F=��CAD����FEA=��BAD�� ���FEA=��F�� ���AEF�ǵ��������Σ�
������
��������������������ȸ��ݵ��������εױ��ϵ����ߺ�һ�����ɵã�ADΪ��BAC�Ľ�ƽ���ߣ�����ƽ���ߵ����ʵó���F=��CAD����FEA=��BAD���Ӷ���FEA=��F���ó����������Σ�
�����������AB=AC��AD��BC�� ���BAD=��CAD�� �֡�AD��EF��
���F=��CAD����FEA=��BAD�� ���FEA=��F�� ���AEF�ǵ��������Σ� ��a<b���ķ���Ӧ�ǣ� ��
A��a��b B��a>b C��a=b D��a=b��a>b
 D
��������
������������ݷ�֤���IJ��裬ֱ�ӵó����ɣ�
��a
D
��������
������������ݷ�֤���IJ��裬ֱ�ӵó����ɣ�
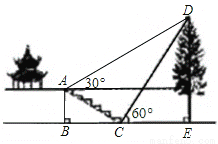
��a��ͼ��ijУ�ۺ�ʵ���С���ͬѧ����������һ����DE�ĸ߶ȣ��������������ǰ��һ��¥ͤǰ��̨����A�㴦���������D������Ϊ30�㣬����������ķ����ߵ�̨���µĵ�C�������������D������Ϊ60�㣮��֪A��ĸ߶�ABΪ2�ף�̨��AC���¶�Ϊ1�� ����AB��BC=1��
����AB��BC=1�� ������B��C��E������ͬһ��ֱ���ϣ�������������������DE�ĸ߶ȣ��������ĸ߶Ⱥ��Բ��ƣ���
������B��C��E������ͬһ��ֱ���ϣ�������������������DE�ĸ߶ȣ��������ĸ߶Ⱥ��Բ��ƣ���
 ��������
��Ϊֱ��������ABC�У�BC=��AB=4�� ����BC=4����DF=x��
��ֱ��������AFD�У�
,
��ֱ��������DCE�У�
,
����
����DE=�ס�
���������������������AF��AB�����ı���ABEFΪ���Σ���DE=x����Rt��CDE�У�CE�T==����Rt��ABC�У��õ������BC����Rt��AFD�У����AF����AF=BC+CE�������x�ij���...
��������
��Ϊֱ��������ABC�У�BC=��AB=4�� ����BC=4����DF=x��
��ֱ��������AFD�У�
,
��ֱ��������DCE�У�
,
����
����DE=�ס�
���������������������AF��AB�����ı���ABEFΪ���Σ���DE=x����Rt��CDE�У�CE�T==����Rt��ABC�У��õ������BC����Rt��AFD�У����AF����AF=BC+CE�������x�ij���... ��ͼ��Ϊ����һ������洹ֱ����OA�ĸ߶ȣ��ھ������ĵ�30��B�����������A�����ǡ�ABOΪ��������OA�ĸ߶�Ϊ( )
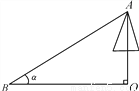
A. 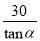 �� B. 30sin���� C. 30tan���� D. 30cos����
�� B. 30sin���� C. 30tan���� D. 30cos����
 C
�������������������Rt��ABO��
��BO=30�ף���ABOΪ����
��AO=BOtan��=30tan�����ף���
��ѡC��
C
�������������������Rt��ABO��
��BO=30�ף���ABOΪ����
��AO=BOtan��=30tan�����ף���
��ѡC�� ��ͼ�������Ľ����������ߣ�������y= 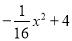 ��ʾ������������˫�е�����Ϊ3m����ôÿ���е����ǣ�������
��ʾ������������˫�е�����Ϊ3m����ôÿ���е����ǣ�������
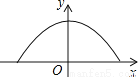
A. ������4m B. ǡ��4m C. ��С��4m D. ����4m��С��8m
 A
����������y=3����y= �еã�
x=4��x= -4����ȥ����
��ÿ���е���Ӧ������4m��
��ѡA��
�㾦�����⿼����κ�����ʵ��Ӧ�ã�����Ϊ��ѧ��ģ�⣬�������κ������ʵ�����⣮�������֪��ֱ�Ӱ�y=3�������ʽ��⼴�ɣ�
A
����������y=3����y= �еã�
x=4��x= -4����ȥ����
��ÿ���е���Ӧ������4m��
��ѡA��
�㾦�����⿼����κ�����ʵ��Ӧ�ã�����Ϊ��ѧ��ģ�⣬�������κ������ʵ�����⣮�������֪��ֱ�Ӱ�y=3�������ʽ��⼴�ɣ� �������µ�������y��(m2��2)x2��2mx��1�ĶԳ��ᾭ����(��1��3)����m��_____��
 ��1
������������������y=��m2-2��x2+2mx+1�ĶԳ��ᾭ���㣨-1��3����
��Գ���Ϊֱ��x=-1��x==-1��
���m1=-1��m2=2��
���������ߵĿ������£����Ե�m=2ʱ��m2-2=2��0���������⣬Ӧ��ȥ��
��m=-1��
�ʴ�Ϊ��-1.
��1
������������������y=��m2-2��x2+2mx+1�ĶԳ��ᾭ���㣨-1��3����
��Գ���Ϊֱ��x=-1��x==-1��
���m1=-1��m2=2��
���������ߵĿ������£����Ե�m=2ʱ��m2-2=2��0���������⣬Ӧ��ȥ��
��m=-1��
�ʴ�Ϊ��-1. 
