题目内容
15. 二次函数y=ax2+bx+c的图象过点(1,0)(0,3),对称轴x=-1.
二次函数y=ax2+bx+c的图象过点(1,0)(0,3),对称轴x=-1.(1)求函数解析式;
(2)请问(1)中的抛物线经过怎样的平移就可以得到y=ax2的图象?
(3)若图象与x轴交于A、B(A在B左)与y轴交于C,顶点D,求四边形ABCD的面积.
分析 (1)利用抛物线的对称性可知抛物线经过点(-3,0),然后利用待定系数法可求得抛物线的解析式;
(2)将(1)的抛物线解析式化为顶点式,然后进行进行平移即可;
(3)如图所示:四边形ADCB的面积=△AED的面积+梯形DCOE的面积+△OBC的面积.
解答 解:(1)∵抛物线的对称轴为x=-1,
∴抛物线经过点(-3,0).
设抛物线的解析式为y=a(x+3)(x-1),将点(0,3)代入得:-3a=3,解得:a=-1.
∴抛物线的解析式为y=-(x+3)(x-1).
整理得:抛物线的解析式为y=-x2-2x+3.
(2)y=-x2-2x+3=-(x2+2x+1-1)+3=-(x+1)2+4,
∴将抛物线向右平移一个单位长度,再向下平移4个单位长度可得到y=-x2的图象.
(3)如图所示: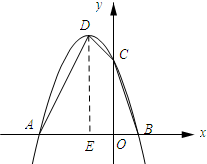
由(2)可知点D的坐标为(-1,4).
四边形ADCB的面积=△AED的面积+梯形DCOE的面积+△OBC的面积
=$\frac{1}{2}AE•DE$+$\frac{1}{2}(ED+OE)•EO$+$\frac{1}{2}OB•OC$
=$\frac{1}{2}×2×4+\frac{1}{2}×(4+3)×1+\frac{1}{2}×1×3$
=4+$\frac{7}{2}$+$\frac{3}{2}$
=9.
点评 本题主要考查的是求二次函数的解析式、平移与坐标变化、不规则图形的面积,将不规则图形的面积转化规则图形的面积是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.计算(-4)2×$\frac{1}{2}$的结果是( )
| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
3.下列计算正确的是( )
| A. | x5-x4=x | B. | 23=6 | C. | -(2x+3)=2x-3 | D. | -x3+3x3=2x3 |
20.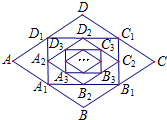 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )
 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{2}$ | D. | 5 |
5.下列命题为假命题的是( )
| A. | 有两条边和一个角对应相等的两个三角形全等 | |
| B. | 对顶角相等 | |
| C. | 三角形的两边之和大于第三边 | |
| D. | 两直线平行,内错角相等 |