题目内容
20.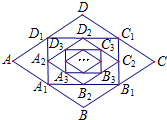 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{2}$ | D. | 5 |
分析 根据题意求出菱形ABCD的周长,根据中点四边形的性质得到A12B12C12D12是菱形,根据题意总结规律得到答案.
解答 解:根据中点四边形的性质可知,A1B1C1D1、A3B3C3D3…是矩形,
A2B2C2D2、A4B4C4D4…是菱形,
∵菱形ABCD的周长是10×4=40,
∴菱形A2B2C2D2的周长是40×$\frac{1}{2}$,
菱形A4B4C4D4的周长是40×$\frac{1}{{2}^{2}}$,
…
则四边形A12B12C12D12的周长是40×$\frac{1}{{2}^{6}}$=$\frac{40}{64}$=$\frac{5}{8}$,
故选:B.
点评 本题考查的是中点四边形的知识,掌握三角形中位线定理和矩形、菱形的判定定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列等式不成立的是( )
| A. | 6$\sqrt{2}$×$\sqrt{3}=6$$\sqrt{6}$ | B. | $\sqrt{8}$$÷\sqrt{2}=2$ | C. | $\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$ | D. | $\sqrt{8}-\sqrt{2}=2$ |
9.若方程4x2-(m-2)x+1=0的左边可以写成一个完全平方式,则m的值为( )
| A. | -2 | B. | -2或6 | C. | -2或-6 | D. | 2或-6 |

 二次函数y=ax2+bx+c的图象过点(1,0)(0,3),对称轴x=-1.
二次函数y=ax2+bx+c的图象过点(1,0)(0,3),对称轴x=-1.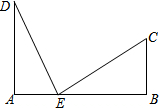 如图,铁路上A,B两点相距23km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=8km.现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
如图,铁路上A,B两点相距23km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=8km.现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?