题目内容
19.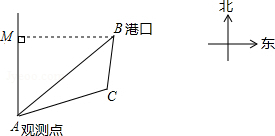 已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10$\sqrt{2}$km,一艘货轮从B港口沿如图所示的BC方向航行4$\sqrt{7}$km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10$\sqrt{2}$km,一艘货轮从B港口沿如图所示的BC方向航行4$\sqrt{7}$km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.| A. | 8$\sqrt{3}$ | B. | 9$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 7$\sqrt{3}$ |
分析 根据∠MAB=45°,BM=10$\sqrt{2}$和勾股定理求出AB的长,再根据tan∠BAD=$\frac{BD}{AD}$,求出BD的长,即可得出AD以及CD的长,进而得出答案.
解答 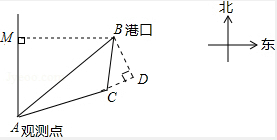 解:∵∠MAB=45°,BM=10$\sqrt{2}$,
解:∵∠MAB=45°,BM=10$\sqrt{2}$,
∴AB=$\sqrt{B{M}^{2}+M{A}^{2}}$=$\sqrt{(10\sqrt{2})^{2}+(10\sqrt{2})^{2}}$=20km,
过点B作BD⊥AC,交AC的延长线于D,
在Rt△ADB中,∠BAD=∠MAC-∠MAB=75°-45°=30°,
tan∠BAD=$\frac{BD}{AD}$=$\frac{\sqrt{3}}{3}$,
∴AD=$\sqrt{3}$BD,
BD2+AD2=AB2,即BD2+($\sqrt{3}$BD)2=202,
∴BD=10,
∴AD=10$\sqrt{3}$,
在Rt△BCH中,BD2+CD2=BC2,BC=4$\sqrt{7}$,
∴CD=2$\sqrt{3}$,
∴AC=AD-CD=10$\sqrt{3}$-2$\sqrt{3}$=8$\sqrt{3}$km,
答:此时货轮与A观测点之间的距离AC的长为8$\sqrt{3}$km.
故选A.
点评 此题主要考查了解直角三角形中方向角问题,根据题意作出辅助线,构造直角三角形,求出BD的长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列四个实际问题中的两个变量之间关系中,属于正比例函数关系的是( )
| A. | 有一个边长为x的正方体,则它的表面积S与边长x之间的函数关系 | |
| B. | 某梯形的下底5cm,高3cm,上底xcm(0<x<5),则梯形的面积S与上底x之间的函数关系 | |
| C. | 一个质量为100kg的物体,静止放在桌面上,则该物体对桌面的压强P与受力面面积S之间的函数关系 | |
| D. | 一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加2m/s,则小球速度v与时间t之间的函数关系 |
14.已知等腰三角形的周长等于20,那么底边长y与腰长x的函数解析式和定义域分别是( )
| A. | y=20-2x(0<x<20) | B. | y=20-2x(0<x<10) | C. | y=20-2x(5<x<10) | D. | y=$\frac{20-x}{2}$(5<x<10) |
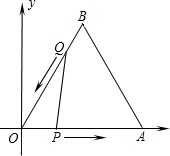 如图,等边△ABO放置在平面直角坐标系中,OA=4,动点P、Q同时从O、B两点出发,分别沿OA、BO方向匀速运动,它们的速度均为每秒1个单位长度,当点P到达点A时,P、Q两点停止运动,设点P的运动时间为x(s)(0<x<4),解答下列问题:
如图,等边△ABO放置在平面直角坐标系中,OA=4,动点P、Q同时从O、B两点出发,分别沿OA、BO方向匀速运动,它们的速度均为每秒1个单位长度,当点P到达点A时,P、Q两点停止运动,设点P的运动时间为x(s)(0<x<4),解答下列问题: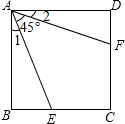 如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论: