题目内容
13.下列说法中,不正确的是( )| A. | 3是(-3)2的算术平方根 | B. | -2与$\sqrt{{{({-2})}^2}}$互为相反数 | ||
| C. | $\sqrt{24}=±2\sqrt{6}$ | D. | $\sqrt{81}$平方根是±3 |
分析 根据开平方,可得平方根,根据相反数的意义,可得答案.
解答 解:A、3是(-3)2的算术平方根,故A不符合题意;
B、-2与$\sqrt{{{({-2})}^2}}$互为相反数,故B不符合题意;
C、$\sqrt{24}$=2$\sqrt{6}$,故C符合题意;
D、$\sqrt{81}$平方根是±3,故D不符合题意;
故选:C.
点评 本题考查了实数的性质,利用开平方是解题关键,注意一个正数只有一个算术平方根,有两个互为相反数的平方根.

练习册系列答案
相关题目
1.ABCD是四边形,AB=2,BC=4,CD=7,则线段AD的取值范围是( )
| A. | 0<AD<7 | B. | 2<AD<7 | C. | 0<AD<13 | D. | 1<AD<13 |
8.已知关于的方程3x-2m+1=0与2-m=2x的解互为相反数,则m=( )
| A. | -$\frac{8}{7}$ | B. | -4 | C. | -3 | D. | $\frac{8}{7}$ |
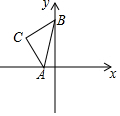 如图,在平面直角坐标系中,△ABC是以C为直角顶点的直角三角形,且AC=BC,点A的坐标为(-1,0),点B的坐标为(0,4),则点C的坐标为(-$\frac{5}{2}$,$\frac{5}{2}$).
如图,在平面直角坐标系中,△ABC是以C为直角顶点的直角三角形,且AC=BC,点A的坐标为(-1,0),点B的坐标为(0,4),则点C的坐标为(-$\frac{5}{2}$,$\frac{5}{2}$).



 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
请从以下两个小题中任选一个作答,若多选,则按第一题计分.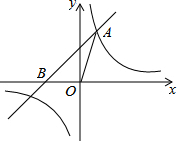 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交x轴于点B.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交x轴于点B. 计算图中阴影部分的面积.
计算图中阴影部分的面积.