题目内容
2.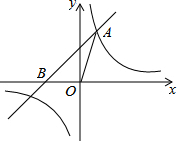 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交x轴于点B.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交x轴于点B.(1)求k和b的值;
(2)求△OAB的面积.
(3)请根据图象直接写出当x取何值时,一次函数值大于反比例函数值.
分析 (1)只需把点A的坐标代入反比例函数和一次函数的解析式,就可解决问题;
(2)只需求出直线AB与x轴的交点,然后根据三角形面积公式就可解决问题;
(3)观察函数图象即可求解.
解答 解:(1)把A(2,5)分别代入y=$\frac{k}{x}$和y=x+b,得$\left\{\begin{array}{l}{\frac{k}{2}=5}\\{2+b=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=10}\\{b=3}\end{array}\right.$. (2)作AC⊥x轴与点C,由(1)得直线AB的表达式为y=x+3,
(2)作AC⊥x轴与点C,由(1)得直线AB的表达式为y=x+3,
∴点B的坐标为(-3,0),
OB=3,
点A的坐标是(2,5).
∴AC=5,
∴△OAB的面积=$\frac{1}{2}$OB•AC=$\frac{1}{2}$×3×5=$\frac{15}{2}$.
(3)由图象可知-5<x<0 或 x>2.
点评 本题主要考查了直线与反比例函数图象上点的坐标特征、运用待定系数法求直线与反比例函数的解析式、解方程组等知识.

练习册系列答案
相关题目
13.下列说法中,不正确的是( )
| A. | 3是(-3)2的算术平方根 | B. | -2与$\sqrt{{{({-2})}^2}}$互为相反数 | ||
| C. | $\sqrt{24}=±2\sqrt{6}$ | D. | $\sqrt{81}$平方根是±3 |
 如图,直线AB、CD相交于O,∠AOC=28°,OE平分∠AOD,求∠EOC的度数.
如图,直线AB、CD相交于O,∠AOC=28°,OE平分∠AOD,求∠EOC的度数.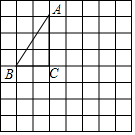 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.