题目内容
8.已知关于的方程3x-2m+1=0与2-m=2x的解互为相反数,则m=( )| A. | -$\frac{8}{7}$ | B. | -4 | C. | -3 | D. | $\frac{8}{7}$ |
分析 表示出方程的解,由两方程解互为相反数求出m的值即可.
解答 解:方程3x-2m+1=0,解得:x=$\frac{2m-1}{3}$,
2-m=2x,解得:x=$\frac{2-m}{2}$,
由题意得:$\frac{2m-1}{3}$+$\frac{2-m}{2}$=0,
去分母得:4m-2+6-3m=0,
解得:m=-4,
故选B
点评 此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.

练习册系列答案
相关题目
18.一条关于数学学习方法的微博在一周内转发了318000次,将318000用科学记数法可以表示为( )
| A. | 3.18×105 | B. | 31.8×105 | C. | 318×104 | D. | 3.18×104 |
3.如图是若干个边长均为1cm的正方形组成的网格,正方形的顶点也叫格点,如果一个多边形的顶点全是格点,这个多边形叫格点多边形,这样的多边形的面积计算起来很方便,只要数一下多边形各边上格点数的总和及这个多边形内的格点数就可以用公式计算,现在我们就来探究这个公式.
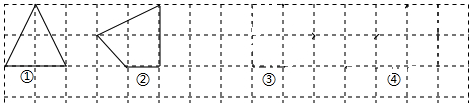
探究一 格点多边形内只有一个格点. 请根据图形填写下列表格
探究二 格点多边形内只有两个格点
请在网格中画出符合条件的两个格点多边形,根据你画出的图形,完善表格中相应的内容.
探究三 当格点多边形内只有三个格点并且各边上格点数的总和为n个时,格点多边形的面积S=$\frac{1}{2}$n+2(用含n的代数式表示)
猜想 当格点多边形内有m个格点并且各边上格点总数的和为n个时,格点多边形的面积S=$\frac{1}{2}$n+m-1(用含m,n的代数式表示)

探究一 格点多边形内只有一个格点. 请根据图形填写下列表格
探究二 格点多边形内只有两个格点
请在网格中画出符合条件的两个格点多边形,根据你画出的图形,完善表格中相应的内容.
| 图形编号 | 多边形内格点数/个 | 多边形各边上格点数的总和/个 | 多边形的面积/cm2 |
| ① | 1 | 4 | 2 |
| ② | 1 | 5 | $\frac{5}{2}$ |
| ③ | 2 | 10 | 6 |
| ④ | 2 | 4 | 3 |
猜想 当格点多边形内有m个格点并且各边上格点总数的和为n个时,格点多边形的面积S=$\frac{1}{2}$n+m-1(用含m,n的代数式表示)
13.下列说法中,不正确的是( )
| A. | 3是(-3)2的算术平方根 | B. | -2与$\sqrt{{{({-2})}^2}}$互为相反数 | ||
| C. | $\sqrt{24}=±2\sqrt{6}$ | D. | $\sqrt{81}$平方根是±3 |
20.已知两个相似三角形的面积之比是4:9,那么这两个三角形周长的比是( )
| A. | 4:9 | B. | 9:4 | C. | 16:81 | D. | 2:3 |
18.下列二次根式中,能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{48}$ | C. | $\sqrt{6}$ | D. | $\sqrt{32}$ |
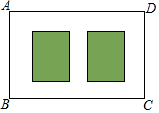 要对一块长90米,宽40米的矩形荒地ABCD进行绿化和硬化,设计方案如图所示,矩形P,Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽度都相等,并使两块绿地面积的和为矩形ABCD面积的$\frac{1}{3}$,求P、Q两块绿地周围的硬化路面的宽.
要对一块长90米,宽40米的矩形荒地ABCD进行绿化和硬化,设计方案如图所示,矩形P,Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽度都相等,并使两块绿地面积的和为矩形ABCD面积的$\frac{1}{3}$,求P、Q两块绿地周围的硬化路面的宽.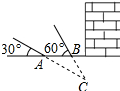 如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C处与地面的距离.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C处与地面的距离.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)