题目内容
8. 设正方形网格的每个小正方形的边长为1,格点△ABC中,AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$.
设正方形网格的每个小正方形的边长为1,格点△ABC中,AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$.(1)请在正方形网格中画出格点△ABC;
(2)这个三角形ABC的面积为$\frac{7}{2}$.
分析 (1)由于$\sqrt{5}$=$\sqrt{{1}^{2}+{2}^{2}}$,$\sqrt{10}$=$\sqrt{{1}^{2}+{3}^{2}}$,$\sqrt{13}$=$\sqrt{{2}^{2}+{3}^{2}}$,然后利用网格特征可写出AB、BC、AC,从而得到△ABC;
(2)用一个矩形的面积分别减取三个直角三角形的面积可计算出△ABC的面积.
解答 解:(1)如图,△ABC为所作;
(2)△ABC的面积=3×3-$\frac{1}{2}$×3×1-$\frac{1}{2}$×3×2-$\frac{1}{2}$×2×1=$\frac{7}{2}$.
故答案为$\frac{7}{2}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
3. 如图,方格纸中的每个小正方形的边长为1,则图中的格点四边形ABCD的面积为( )
如图,方格纸中的每个小正方形的边长为1,则图中的格点四边形ABCD的面积为( )
 如图,方格纸中的每个小正方形的边长为1,则图中的格点四边形ABCD的面积为( )
如图,方格纸中的每个小正方形的边长为1,则图中的格点四边形ABCD的面积为( )| A. | 3.5 | B. | 5 | C. | 5.5 | D. | 4.5 |
18.下列函数是反比例函数的是( )
| A. | y=$\frac{x}{3}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{1}{x-1}$ | D. | y=$\frac{1}{x}$+1 |
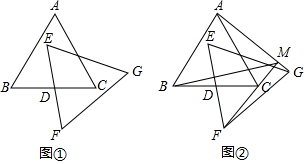 已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点.
已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点.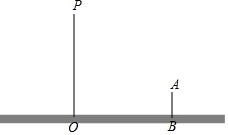 晚上,小亮在广场乘凉,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯
晚上,小亮在广场乘凉,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯