题目内容
20.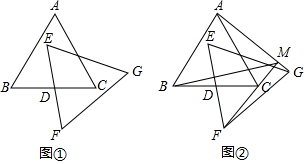 已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点.
已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点.(Ⅰ)如图①,这两个等边三角形的高为2$\sqrt{3}$;
(Ⅱ)如图②,直线AG,FC相交于点M,当△EFG绕点D旋转时,线段BM长的最小值是2$\sqrt{3}$-2.
分析 (Ⅰ)如图①中,连接AD,在Rt△ABD中,利用勾股定理即可解决问题.
(Ⅱ)如图①中,连接AE、EC、CG.首先证明∠AMF=90°,在如图②中,当点M运动到BM⊥AC时,BM最短,由此即可解决问题.
解答 解:(Ⅰ)如图①中,连接AD,
∵△ABC是等边三角形,BD=CD,
∴AD⊥BC,
在Rt△ABD中,∵AB=4,BD=2,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
故答案为2$\sqrt{3}$.
(Ⅱ)如图①中,连接AE、EC、CG.
∵DE=DF=DC,
∴△EFC是直角三角形,
∴∠ECF=90°,
∵∠ADC=∠EDG=90°,
∴∠ADE=∠GDC,
在△ADE和△GDC中,
$\left\{\begin{array}{l}{DA=DG}\\{∠ADE=∠GDC}\\{DE=DC}\end{array}\right.$,
∴△ADE≌△GDC,
∴AE=CG,∠DAE=∠DGC,
∵DA=DG,
∴∠DAG=∠DGA,
∴∠GAE=∠AGC,
∵AG=GA,
∴△AGE≌△GAC,
∴∠GAK=∠AGK,
∴KA=KG,∵AC=EG,
∴EK=KC,
∴∠KEC=∠KCE,
∵∠AKG=∠EKC,
∴∠KAG=∠KCE,
∴EC∥AG,
∴∠AMF=∠ECF=90°,
∴点M在以AC为直径的圆上运动,
如图②中,当点M运动到BM⊥AC时,BM最短,
∵OB=2$\sqrt{3}$,AO=OM=OC=2,
∴BM的最小值为2$\sqrt{3}$-2.
故答案为2$\sqrt{3}$-2.
点评 本题考查旋转的性质、等边三角形的判定和性质、全等三角形的判定和性质、圆的有关知识等知识,解题的关键是证明∠AMF=90°,判断出点M在以AC为直径的圆上运动,属于中考常考题型.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案| A. | 4x=2 | B. | 3x+6=0 | C. | $\frac{1}{3}$x=3 | D. | 7x-14=0 |
 设正方形网格的每个小正方形的边长为1,格点△ABC中,AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$.
设正方形网格的每个小正方形的边长为1,格点△ABC中,AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$.
 某中学为了解学生上学方式,现随机抽取部分学生进行调查,将结果绘成条形统计图如图,由此可估计该校2000名学生中有260名学生是乘车上学的.
某中学为了解学生上学方式,现随机抽取部分学生进行调查,将结果绘成条形统计图如图,由此可估计该校2000名学生中有260名学生是乘车上学的.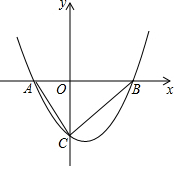 如图,已知二次函数y=x2-($\sqrt{3}$-m)x-$\sqrt{3}$m(其中0<m<$\sqrt{3}$)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,△ABC的外心为P.
如图,已知二次函数y=x2-($\sqrt{3}$-m)x-$\sqrt{3}$m(其中0<m<$\sqrt{3}$)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,△ABC的外心为P.