题目内容
19．在平面直角坐标系中，抛物线y=（x+2）2-3与y轴的交点坐标是（0，1）．分析 令x=0，求出y的值，即可求出抛物线与y轴的交点坐标．
解答 解：令抛物线y=（x+2）2-3中x=0，
即y=4-3=1，
则抛物线y=（x+2）2-3与y轴的交点坐标是（0，1），
故答案为（0，1）．
点评 本题主要考查了二次函数图象上点的坐标特征，解题的关键是令x=0，求出y的值，此题难度不大．
练习册系列答案
相关题目
14．|-2017|的值是（ ）
| A． | $-\frac{1}{2017}$ | B． | -2017 | C． | 2017 | D． | $\frac{1}{2017}$ |
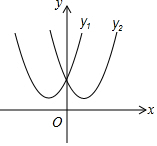定义感知：我们把顶点关于y轴对称，且交于y轴上同一点的两条抛物线叫做“孪生抛物线”，如图所示的抛物线y1=x2+2x+2与y2=x2-2x+2是一对“孪生抛物线”．
14．数轴上的点A到原点的距离为5，则点A表示的数是（ ）
| A． | 5 | B． | -5 | C． | ±5 | D． | -5或5 |
设正方形网格的每个小正方形的边长为1，格点△ABC中，AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$．
某中学为了解学生上学方式，现随机抽取部分学生进行调查，将结果绘成条形统计图如图，由此可估计该校2000名学生中有260名学生是乘车上学的．