题目内容
7.若反比例函数y=$\frac{1-3m}{x}$的图象在第一象限内,y随x的增大而减小,则m的取值范围是m<$\frac{1}{3}$,图象位于第一、三象限.分析 先根据反比例函数图象所在的每个象限内,y的值随x的增大而减小判断出1-3m的符号,求出m的取值范围即可.
解答 解:∵反比例函数y=$\frac{1-3m}{x}$的图象在第一象限内,y随x的增大而减小,
∴1-3m>0,
解得m<$\frac{1}{3}$.
由反比例函数的对称性,该函数图象位于第一、三象限.
故答案是:m<$\frac{1}{3}$;一、三.
点评 本题考查的是反比例函数的性质,即反比例函数y=$\frac{k}{x}$(k≠0)的图象是双曲线;当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
18.已知等腰三角形的顶角为140°,那么它一腰上的高与底边的夹角为( )
| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
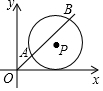 如图,在平面直角坐标系中,点P的坐标为(a,5),半径为5的⊙P交直线y=x于点A,B,若弦AB=8,-则a的值为5+3$\sqrt{2}$.
如图,在平面直角坐标系中,点P的坐标为(a,5),半径为5的⊙P交直线y=x于点A,B,若弦AB=8,-则a的值为5+3$\sqrt{2}$.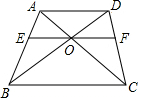 四边形ABCD中,AD∥BC,AC与BD相交于O点,过O点作EF∥BC分别交AB、CD于E,F两点,求证:
四边形ABCD中,AD∥BC,AC与BD相交于O点,过O点作EF∥BC分别交AB、CD于E,F两点,求证: