Question

12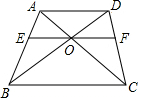．四边形ABCD中，AD∥BC，AC与BD相交于O点，过O点作EF∥BC分别交AB、CD于E，F两点，求证：
（1）OE=OF；
（2）$\frac{1}{AD}$+$\frac{1}{BC}$=$\frac{2}{EF}$．

Answer 1

分析 （1）先由平行得出对应边成比例，再根据平行线分线段成比例定理，得出EO：BC=FO：BC，即可得出O是EF的中点；
（2）先由AD∥BC∥EF，得到△CFO∽△CDA，△AOE∽△ACB，进而得出FO：AD=CO：AC，OE：BC=AO：AC，最后两式相加变形，可得结论．

解答 证明：（1）∵AD∥BC，
∴DO：DB=AO：AC，
又∵FO：BC=DO：DB，EO：BC=AO：AC，
∴EO：BC=FO：BC，
∴O是EF的中点，
∴OE=OF；

（2）∵AD∥BC∥EF，
∴△CFO∽△CDA，且△AOE∽△ACB，
∴FO：AD=CO：AC，且OE：BC=AO：AC，
两式相加，可得
$\frac{FO}{AD}$+$\frac{OE}{BC}$=$\frac{CO}{AC}$+$\frac{AO}{AC}$=$\frac{AC}{AC}$=1，
即$\frac{FO}{AD}$+$\frac{OE}{BC}$=1，
又∵OE=OF=$\frac{1}{2}$EF，
∴$\frac{1}{AD}$+$\frac{1}{BC}$=$\frac{1}{\frac{1}{2}EF}$，即$\frac{1}{AD}$+$\frac{1}{BC}$=$\frac{2}{EF}$．

点评 本题主要考查相似三角形的判定与性质以及平行线分线段成比例定理的运用，掌握平行线所分线段对应成比例是解题的关键．