题目内容
18.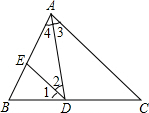 请在括号里填上推理的根据
请在括号里填上推理的根据已知∠1=40°,∠C=40°,∠2=∠4
求证:AD平分∠BAD
证明:∵∠1=40°,∠C=40( 已知 )
∴∠1=∠C(等量代换)
∴AC∥DE(同位角相等,两直线平行)
∴∠2=∠3(两直线平行,内错角相等)
∵∠2=∠4(已知)
∴∠3=∠4(等量代换)
∴AD平分∠BAD(角平分线定义.
分析 求出∠1=∠C,根据平行线的判定得出AC∥DE,根据平行线的性质得出∠2=∠3,求出∠3=∠4即可.
解答 证明:∵∠1=40°,∠C=40( 已知 )
∴∠1=∠C (等量代换),
∴AC∥DE (同位角相等,两直线平行),
∴∠2=∠3 (两直线平行,内错角相等),
∵∠2=∠4 (已知),
∴∠3=∠4 (等量代换),
∴AD平分∠BAD(角平分线定义),
故答案为:(等量代换),(同位角相等,两直线平行),(两直线平行,内错角相等),(已知),(等量代换),(角平分线定义).
点评 本题考查了平行线的性质和判定,角平分线定义的应用,能正确运用平行线的性质和判定定理进行推理是解此题的关键,注意:平行线的性质是:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
相关题目
6.点A(-8,6)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.己知菱形ABCD的边长是6,∠ADC=120°,点E在直线AD上,DE=3,连接BE与对角线AC相交于点M,则线段CM的长是4$\sqrt{3}$或$\frac{12\sqrt{3}}{5}$.
7.若数据8、4、x、2的平均数是4,则这组数据的中位数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
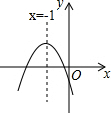 y=ax2+bx+c(a≠0)的图象如图所示,那么下面六个代数式:abc,b2-4ac,a-b+c,a+b+c,2a-b,9a-4b中,值大于0的有( )
y=ax2+bx+c(a≠0)的图象如图所示,那么下面六个代数式:abc,b2-4ac,a-b+c,a+b+c,2a-b,9a-4b中,值大于0的有( )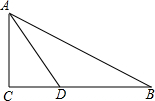 如图,△ABC中,∠C=90°,AD平分∠BAC,CD=$\frac{10}{3}$,BC=12,AB=13,则△ADB的面积是$\frac{65}{3}$.
如图,△ABC中,∠C=90°,AD平分∠BAC,CD=$\frac{10}{3}$,BC=12,AB=13,则△ADB的面积是$\frac{65}{3}$. 如图,圆锥的母线AB=6,底面半径CB=2,则其侧面展开图扇形的圆心角α=120°.
如图,圆锥的母线AB=6,底面半径CB=2,则其侧面展开图扇形的圆心角α=120°.