题目内容
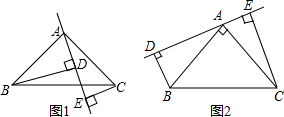
10. 如图,△ABC中,∠C=90°,AD平分∠BAC,CD=$\frac{10}{3}$,BC=12,AB=13,则△ADB的面积是$\frac{65}{3}$.
如图,△ABC中,∠C=90°,AD平分∠BAC,CD=$\frac{10}{3}$,BC=12,AB=13,则△ADB的面积是$\frac{65}{3}$.
分析 过D作DE⊥AB于E,根据角平分线性质求出DE,根据三角形的面积公式求出即可.
解答 解:
过D作DE⊥AB于E,
∵△ABC中,∠C=90°,AD平分∠BAC,CD=$\frac{10}{3}$,
∴CD=DE=$\frac{10}{3}$,
∵AB=13,
∴△ADB的面积是$\frac{1}{2}$×AB×DE=$\frac{1}{2}$×13×$\frac{10}{3}$=$\frac{65}{3}$,
故答案为:$\frac{65}{3}$.
点评 本题考查了角平分线性质和三角形的面积的应用,能求出△ADB的高是解此题的关键,注意:角平分线上的点到角两边的距离相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.点(-2015,2015)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.下列计算中,错误的有( )
①(3a+4)(3a-4)=9a2-4;
②(2a2-b)(2a2+b)=4a2-b;
③(3-x)(x+3)=x2-9;
④(-x+y)(x+y)=-(x-y)(x+y)=-x2-y2.
⑤(3-x)2=(x-3)2=x2-6x+9.
①(3a+4)(3a-4)=9a2-4;
②(2a2-b)(2a2+b)=4a2-b;
③(3-x)(x+3)=x2-9;
④(-x+y)(x+y)=-(x-y)(x+y)=-x2-y2.
⑤(3-x)2=(x-3)2=x2-6x+9.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.分式$\frac{{x}^{2}-9}{x+3}$的值为0,则( )
| A. | x=-3 | B. | x=±3 | C. | x=3 | D. | x=0 |
 如图,已知AB=AC,DE=DF,求证:BE=CF.
如图,已知AB=AC,DE=DF,求证:BE=CF. 请在括号里填上推理的根据
请在括号里填上推理的根据 如图,A、B、C为数轴(单位长度为1)上的三个点,其对应的数据都是整数,若点B对应的数比点A对应的数的2倍大7,那么点C对应的数是3.
如图,A、B、C为数轴(单位长度为1)上的三个点,其对应的数据都是整数,若点B对应的数比点A对应的数的2倍大7,那么点C对应的数是3.