题目内容
15.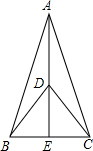 如图,在△ABC中,点E在BC上,点D在AE上,∠ABD=∠ACD,∠BDE=∠CDE.试说明BE=CE.
如图,在△ABC中,点E在BC上,点D在AE上,∠ABD=∠ACD,∠BDE=∠CDE.试说明BE=CE.
分析 要证BE=CE,要先证明△ABD和△ACD全等,得到BD=CD,再证明△BDE和△CDE全等即可.
解答 证明:∵∠ADB=180°-∠BDE,∠ADC=180°-∠CDE,
∴∠ADB=∠ADC.
在△ADB和△ADC中,
$\left\{\begin{array}{l}{∠ABD=∠ACD}\\{∠ADB=∠ADC}\\{AD=AD}\end{array}\right.$,
∴△ADB≌△ADC.
∴BD=CD
∵在△DBE和△DCE中,
$\left\{\begin{array}{l}{BD=CD}\\{∠BDE=∠CDE}\\{DE=DE}\end{array}\right.$,
∴△DBE≌△DCE.
∴BE=CE.
点评 本题主要考查了全等三角形的判定与性质,证明简单的线段相等,可以通过全等三角形来证明.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
4.两圆半径R、r分别是方程x2-3x+2=0的两根,且圆心距d=3,则两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 内含 | D. | 外离或内含 |
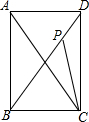 如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠BPC=67.5°,∠ACP=22.5°.
如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠BPC=67.5°,∠ACP=22.5°.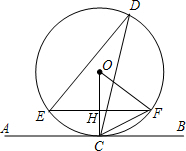 如图,直线AB与⊙O相切于点C,弦EF∥AB交OC于H,D是⊙O上一点,连结DE、DC、OF.
如图,直线AB与⊙O相切于点C,弦EF∥AB交OC于H,D是⊙O上一点,连结DE、DC、OF.  如图,正方形AOCB在平面直角坐标系xOy中,点O为原点,点B在反比例函数y=$\frac{k}{x}$(x>0)图象上,△BOC的面积为8.
如图,正方形AOCB在平面直角坐标系xOy中,点O为原点,点B在反比例函数y=$\frac{k}{x}$(x>0)图象上,△BOC的面积为8.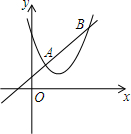 如图,直线y=x+1与抛物线y=x2-2mx+m2+m交于A、B两点(A在B左边).求证:无论m为何值,AB的长总为定值.
如图,直线y=x+1与抛物线y=x2-2mx+m2+m交于A、B两点(A在B左边).求证:无论m为何值,AB的长总为定值.