题目内容
16.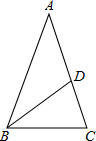 如图,已知:在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则∠ADB的度数是108°.
如图,已知:在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则∠ADB的度数是108°.
分析 由已知根据等腰三角形的性质易得两底角的度数,结合角平分线的性质和三角形内角和定理即可求解.
解答 解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=(180°-36°)÷2=72°,
又∵BD为∠ABC的平分线,
∴∠ABD=36°,
∴∠ADB=180°-(36°+36°)=108°.
故答案为:108°.
点评 本题考查了三角形内角和定理及等腰三角形的性质、角平分线的性质;综合运用各种知识是解答本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
4.两圆半径R、r分别是方程x2-3x+2=0的两根,且圆心距d=3,则两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 内含 | D. | 外离或内含 |
11.已知y=(k-2)x|k|-1+2k-3是关于x的一次函数,则k的值是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
8.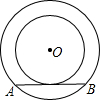 如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )
如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )
 如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )
如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 16cm |
6.下面的计算正确的是( )
| A. | 3x2•5x2=15x2 | B. | x3•x5=x15 | C. | x5÷x=x4 | D. | (x5)3=x8 |
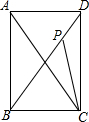 如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠BPC=67.5°,∠ACP=22.5°.
如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠BPC=67.5°,∠ACP=22.5°.