题目内容
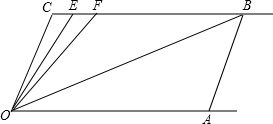 如图,已知直线CB∥OA,∠C=∠OAB=100°,E,F在BC上,满足∠FOB=∠AOB,OE平分∠COF.
如图,已知直线CB∥OA,∠C=∠OAB=100°,E,F在BC上,满足∠FOB=∠AOB,OE平分∠COF.(1)求∠EOB的度数;
(2)若平行移动AB,则∠OBC:∠OFC的值是否发生变化?若变化找出变化规律,若不变求其比值.
考点:平行线的性质
专题:计算题,几何图形问题
分析:(1)先根据平行线的性质得出∠COA的度数与∠FBO=∠AOB,再由∠FOB=∠AOB,得出∠FBO=∠FOB即OB平分∠AOF,根据OE平分∠COF,可知∠EOB=∠EOF+∠FOB,故可得出结论;
(2)根据平行线的性质可得出∠OBC=∠BOA,∠OFC=∠FOA,从而得出答案.
(2)根据平行线的性质可得出∠OBC=∠BOA,∠OFC=∠FOA,从而得出答案.
解答:解:(1)∵CB∥OA,∠C=∠OAB=100°,
∴∠COA=180°-∠C=180°-100°=80°,∠FBO=∠AOB,
又∵∠FOB=∠AOB,
∴∠FBO=∠FOB,
∴OB平分∠AOF,
又∵OE平分∠COF,
∴∠EOB=∠EOF+∠FOB=
∠COA=
×80°=40°;
(2)不变,
∵CB∥OA,
∴∠OBC=∠BOA,∠OFC=∠FOA,
∴∠OBC:∠OFC=∠AOB:∠FOA,
又∵∠FOA=∠FOB+∠AOB=2∠AOB,
∴∠OBC:∠OFC=∠AOB:∠FOA=∠AOB:2∠AOB=1:2,
∴∠COA=180°-∠C=180°-100°=80°,∠FBO=∠AOB,
又∵∠FOB=∠AOB,
∴∠FBO=∠FOB,
∴OB平分∠AOF,
又∵OE平分∠COF,
∴∠EOB=∠EOF+∠FOB=
| 1 |
| 2 |
| 1 |
| 2 |
(2)不变,
∵CB∥OA,
∴∠OBC=∠BOA,∠OFC=∠FOA,
∴∠OBC:∠OFC=∠AOB:∠FOA,
又∵∠FOA=∠FOB+∠AOB=2∠AOB,
∴∠OBC:∠OFC=∠AOB:∠FOA=∠AOB:2∠AOB=1:2,
点评:本题主要考查了平行线、角平分线的性质以及平行四边形的性质,有一定的综合性,难度适中.

练习册系列答案
相关题目
 如图,直线AB、CD、EF都经过点O,且AB⊥CD,∠COE=35°,求∠EOB、∠BOF的度数.
如图,直线AB、CD、EF都经过点O,且AB⊥CD,∠COE=35°,求∠EOB、∠BOF的度数. 如图所示,将三角形ABC按要求画出平移后的三角形A′B′C′.
如图所示,将三角形ABC按要求画出平移后的三角形A′B′C′. 如图,已知AB∥ED,x=∠A+∠E,y=∠B+∠C+∠D,探求x与y的数量关系.
如图,已知AB∥ED,x=∠A+∠E,y=∠B+∠C+∠D,探求x与y的数量关系. 如图,四边形OABC是长方形,顶点坐标为A(6,0),B(6,4),C(0,4),O(0,0),线段AB,BC中点分别为M,N.
如图,四边形OABC是长方形,顶点坐标为A(6,0),B(6,4),C(0,4),O(0,0),线段AB,BC中点分别为M,N. 如图,已知AB∥CD,AB=CD,AD∥BC,AD=BC,DE是∠ADC的角平分线,交BC于点E.
如图,已知AB∥CD,AB=CD,AD∥BC,AD=BC,DE是∠ADC的角平分线,交BC于点E.