题目内容
 如图,已知AB∥CD,AB=CD,AD∥BC,AD=BC,DE是∠ADC的角平分线,交BC于点E.
如图,已知AB∥CD,AB=CD,AD∥BC,AD=BC,DE是∠ADC的角平分线,交BC于点E.(1)求证:CD=CE;
(2)若AE⊥DE,DC=5,DE=8,求四边形ABCD的面积.
考点:勾股定理
专题:几何图形问题,证明题
分析:(1)根据角平分线的定义可得∠1=∠2,根据平行四边形的对边平行可得AD∥BC,再根据两直线平行,内错角相等可得∠1=∠3,从而求出∠2=∠3,然后利用等角对等边证明即可;
(2)作EF∥CD,则F是AD的中点,易证四边形EFDC是菱形,根据勾股定理求得CF的长,然后利用菱形的面积公式即可求得菱形EFDC的面积,四边形ABCD的面积是菱形EFDC的面积的2倍,据此即可求解.
(2)作EF∥CD,则F是AD的中点,易证四边形EFDC是菱形,根据勾股定理求得CF的长,然后利用菱形的面积公式即可求得菱形EFDC的面积,四边形ABCD的面积是菱形EFDC的面积的2倍,据此即可求解.
解答: (1)证明:∵DE是∠ADC的角平分线,
(1)证明:∵DE是∠ADC的角平分线,
∴∠1=∠2,
在平行四边形ABCD中,AD∥BC,
∴∠1=∠3,
∴∠2=∠3,
∴CD=CE;
(2)解:∵AB∥CD,
∴∠BAD+∠ADC=180°,
∴
∠BAD+
∠ADC=90°,
又∵∠1=
∠ADC,在直角△ADE中,∠EAD+∠1=90°,
∴∠EAD=
∠BAD,
即AE是∠BAD的平分线.
同(1)可得BE=AB=CD=5,
作EF∥CD,则F是AD的中点,
又∵AD∥BC,EC=CD,
∴四边形EFDC是菱形.
∴DE⊥CF,DG=
DE=4,
在直角△CDG中,CG=
=
=3.
∴CF=2CG=6,
∴菱形EFDC的面积是:
DE•CF=
×8×6=24,
∴四边形ABCD的面积是2×24=48.
 (1)证明:∵DE是∠ADC的角平分线,
(1)证明:∵DE是∠ADC的角平分线,∴∠1=∠2,
在平行四边形ABCD中,AD∥BC,
∴∠1=∠3,
∴∠2=∠3,
∴CD=CE;
(2)解:∵AB∥CD,
∴∠BAD+∠ADC=180°,
∴
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠1=
| 1 |
| 2 |
∴∠EAD=
| 1 |
| 2 |
即AE是∠BAD的平分线.
同(1)可得BE=AB=CD=5,
作EF∥CD,则F是AD的中点,
又∵AD∥BC,EC=CD,
∴四边形EFDC是菱形.
∴DE⊥CF,DG=
| 1 |
| 2 |
在直角△CDG中,CG=
| CD2-DG2 |
| 52-42 |
∴CF=2CG=6,
∴菱形EFDC的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形ABCD的面积是2×24=48.
点评:本题考查了菱形的判定与性质,以及等腰三角形的判定方法,正确理解四边形EFDC是菱形,边形ABCD的面积是菱形EFDC的面积的2倍是关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
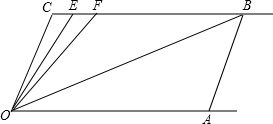 如图,已知直线CB∥OA,∠C=∠OAB=100°,E,F在BC上,满足∠FOB=∠AOB,OE平分∠COF.
如图,已知直线CB∥OA,∠C=∠OAB=100°,E,F在BC上,满足∠FOB=∠AOB,OE平分∠COF.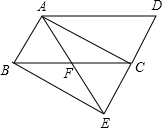 如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F. 如图,在三角形ABC中,CD平分∠ACB,DE∥AC交BC于E,EF∥CD交AB于F.求证:EF平分∠DEB.
如图,在三角形ABC中,CD平分∠ACB,DE∥AC交BC于E,EF∥CD交AB于F.求证:EF平分∠DEB. 已知实数a、b、c在数轴上的对应点的位置如图所示,试化简:
已知实数a、b、c在数轴上的对应点的位置如图所示,试化简: 如图,在三角形ABC中,因为∠1与∠B相等,所以得出DE与BC平行,用数学式子表述为
如图,在三角形ABC中,因为∠1与∠B相等,所以得出DE与BC平行,用数学式子表述为