题目内容
已知m满足
=3,n满足(2k+1)2+
=0,求
的值.
| 2m-1 |
| 3 |
| 91+7n |
| 3 | m2-3n |
考点:立方根,非负数的性质:偶次方,非负数的性质:算术平方根,解一元一次方程
专题:计算题
分析:由m满足
=3,求得m=5;根据非负数的性质由91+7n=0得出n=-13,由此代入代数式求得数值即可.
| 2m-1 |
| 3 |
解答:解:∵m满足
=3,
∴m=5;
∵n满足(2k+1)2+
=0,
∴91+7n=0,
解得n=-13,
∴
=
=
=4.
故答案为:4.
| 2m-1 |
| 3 |
∴m=5;
∵n满足(2k+1)2+
| 91+7n |
∴91+7n=0,
解得n=-13,
∴
| 3 | m2-3n |
| 3 | 52-3×(-13) |
| 3 | 64 |
故答案为:4.
点评:此题考查开立方,非负数的性质,一元一次方程的解法,注意解答的顺序与方法.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=3:2,求∠BOD的度数.
如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=3:2,求∠BOD的度数.
 如图,根据下列语句画图:过点P画射线的垂线,Q为垂足.
如图,根据下列语句画图:过点P画射线的垂线,Q为垂足. 如图,直线CD交于点O,OM是射线.请你指出∠AOC,∠MOB的邻补角,指出∠AOD,∠BOD的对顶角,∠BOM有对顶角吗?
如图,直线CD交于点O,OM是射线.请你指出∠AOC,∠MOB的邻补角,指出∠AOD,∠BOD的对顶角,∠BOM有对顶角吗?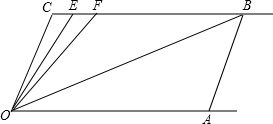 如图,已知直线CB∥OA,∠C=∠OAB=100°,E,F在BC上,满足∠FOB=∠AOB,OE平分∠COF.
如图,已知直线CB∥OA,∠C=∠OAB=100°,E,F在BC上,满足∠FOB=∠AOB,OE平分∠COF.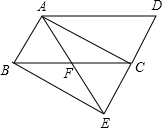 如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F. 已知实数a、b、c在数轴上的对应点的位置如图所示,试化简:
已知实数a、b、c在数轴上的对应点的位置如图所示,试化简: