题目内容
下列条件：①两角及一边分别相等；②两边及其夹角分别相等；③两边及一边所对的角分别相等；④两角及其夹边分别相等．其中能判定两个三角形全等的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
考点：全等三角形的判定
专题：
分析：全等三角形的判定定理有SAS，ASA，AAS，SSS，HL根据定理判定即可．
解答：解：①两角及一边分别相等；能根据AAS判定两个三角形全等，故选项正确；
②两边及其夹角分别相等；能根据SAS判定两个三角形全等，故选项正确；
③两边及一边所对的角分别相等；不能判定两个三角形全等，故选项错误；
④两角及其夹边分别相等；能根据ASA判定两个三角形全等，故选项正确．
综上所述，①②④正确．
故选：C．
②两边及其夹角分别相等；能根据SAS判定两个三角形全等，故选项正确；
③两边及一边所对的角分别相等；不能判定两个三角形全等，故选项错误；
④两角及其夹边分别相等；能根据ASA判定两个三角形全等，故选项正确．
综上所述，①②④正确．
故选：C．
点评：本题考查三角形全等的判定方法．注意：AAA，SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
练习册系列答案
阅读快车系列答案
相关题目
在△ABC中，∠C=90°，△ABC的两锐角平分线AD、BE交于点O．
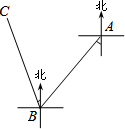一艘轮船由海平面上A地出发向南偏西60°的方向行驶40海里到达B地，再由B地向北偏西30°的方向行驶30海里到达C地，则A、C两地相距（ ）| A、30海里 | B、40海里 |
| C、50海里 | D、60海里 |
抛物线y=3x2向下平移3个单位，再向左平移2个单位，得到的抛物线解析式为（ ）
| A、y=3（x+2）2+3 |
| B、y=3（x-2）2+3 |
| C、y=3（x+2）2-3 |
| D、y=3（x-2）2-3 |
下列是假命题的是（ ）
| A、两点之间，线段最短 |
| B、过一点有且只有一条直线与已知直线垂直 |
| C、直角三角形的两个锐角互余 |
| D、两条直线被第三条直线所截，同位角相等 |
在Rt△ABC，∠C=90°，sinB=
，则sinA的值是（ ）
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法正确的是（ ）
| A、所有的等边三角形都相似 |
| B、所有的菱形都相似 |
| C、所有的等腰三角形都相似 |
| D、所有的矩形都相似 |
下列说法正确的是（ ）
| A、有最大的负整数 |
| B、有最小的负整数 |
| C、小数都能化成分数 |
| D、0是最小的整数 |