Question

2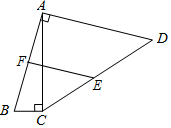．如图，四边形ABCD中，AB=AD，∠ACB=∠BAD=90°，E、F分别为CD、AB的中点，BC=2，CD=2$\sqrt{13}$，则EF=$\sqrt{17}$．

Answer 1

分析 作DN⊥AC垂足为N点，EM⊥AC于M，EG⊥DN于G，FH⊥EG于H交AC于K．由△ABC≌△DAN（AAS），推出BC=AN=2，AC=DN，推出CN=DN-2，在Rt△CDN中，由勾股定理得：CN²+DN²=CD²，即（DN-2）²+DN²=（2$\sqrt{13}$）²，解得：DN=6推出AC=DN=6，CN=4，由四边形NKHG、四边形KMEH是矩形，推出KM=HG，由AF=FB，FK∥BC，推出AK=KC=3，FK=$\frac{1}{2}$BC=1，由EM∥DN，EC=DE，推出CM=MN=2，EM=KH=$\frac{1}{2}$DN=3，推出FH=4，HE=KM=1，在Rt△FHE中，根据EF=$\sqrt{F{H}^{2}+H{E}^{2}}$计算即可角问题．

解答 解：作DN⊥AC垂足为N点，EM⊥AC于M，EG⊥DN于G，FH⊥EG于H交AC于K．

∵∠BAD=∠CAM=90°，
即∠BAC+∠CAD=∠CAD+∠DAN=90°，
∴∠BAC=∠NDA，
在△ABC和△ADM中
$\left\{\begin{array}{l}{∠ACB=∠AND}\\{∠BAC=∠ADN}\\{AB=AD}\end{array}\right.$，
∴△ABC≌△DAN（AAS），
∴BC=AN=2，AC=DN，
∴CN=DN-2，
在Rt△CDN中，由勾股定理得：CN²+DN²=CD²，
即（DN-2）²+DN²=（2$\sqrt{13}$）²，
解得：DN=6或-4（舍弃），
∴AC=DN=6，CN=4，
∵四边形NKHG、四边形KMEH是矩形，
∴KM=HG，
∵AF=FB，FK∥BC，
∴AK=KC=3，FK=$\frac{1}{2}$BC=1，
∵EM∥DN，EC=DE，
∴CM=MN=2，EM=KH=$\frac{1}{2}$DN=3，
∴FH=4，HE=KM=1，
在Rt△FHE中，EF=$\sqrt{F{H}^{2}+H{E}^{2}}$=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$，
故答案为$\sqrt{17}$．

点评 本题考查了全等三角形的判定与性质、三角形的中位线定理、勾股定理、矩形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形和直角三角形解决问题，属于中考填空题中的压轴题．