题目内容
1.一次函数y1=ax+b与一次函数y2=-bx-a在同一平面直角坐标系中的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 首先设定一个为一次函数y1=ax+b的图象,再考虑另一条的a,b的值,看看是否矛盾即可.
解答 解:A、如果过第一二四象限的图象是y1,由y1的图象可知,a<0,b>0;由y2的图象可知,-b>0,-a>0,a<0,b<0,两结论矛盾,故错误;
B、如果过第一二四象限的图象是y1,由y1的图象可知,a<0,b>0;由y2的图象可知,-b>0,-a<0,a>0,b<0;两结论矛盾,故错误;
C、如果过第二三四象限的图象是y1,由y1的图象可知,a<0,b<0;由y2的图象可知,-b<0,-a<0,b>0,a>0,两结论相矛盾,故错误;
D、如果过第一二四象限的图象是y1,由y1的图象可知,a<0,b>0;由y2的图象可知,-b<0,-a>0,b>0,a<0,两结论不矛盾,故正确.
故选D.
点评 此题主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
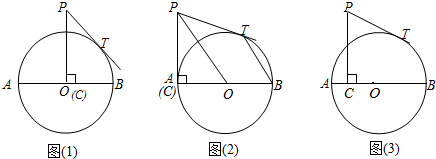




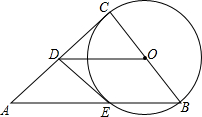 在△ABC中,∠ACB=90°,以BC为直径作圆O,交斜边AB于E,D是AC的中点,连接DE.
在△ABC中,∠ACB=90°,以BC为直径作圆O,交斜边AB于E,D是AC的中点,连接DE.