题目内容
15．顺次连结对角线互相垂直的四边形各边上的中点，得到的新四边形是（ ）| A． | 矩形 | B． | 正方形 | C． | 菱形 | D． | 平行四边形 |
分析 根据四边形对角线互相垂直，运用三角形中位线平行于第三边证明四个角都是直角，判断是矩形．
解答 解：如图：∵E、F、G、H分别为各边中点，
∴EF∥GH∥DB，EF=GH=$\frac{1}{2}$DB，
EH=FG=$\frac{1}{2}$AC，EH∥FG∥AC，
∵DB⊥AC，
∴EF⊥EH，
∴四边形EFGH是矩形．
故选：A．
点评 本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边且等于第三边的一半是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，将△ABC沿BC方向平移4cm得到△DEF，若△ABC的周长为20cm，则四边形ABFD的周长为28cm．
6．
如图，AB∥EF∥CD，∠ABC=46°，∠BCE=20°，则∠CEF=（ ）
如图，AB∥EF∥CD，∠ABC=46°，∠BCE=20°，则∠CEF=（ ）| A． | 144° | B． | 154° | C． | 164° | D． | 160° |
如图，直线AB、CD、EF互相平行，且∠ABE=50°，∠ECD=150°，则∠BEC=20°．
已知，在△ABC中，AB=AC=a，M为底边BC上任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．
7．
如图，∠ADE=∠ACB，且$\frac{AD}{AC}$=$\frac{2}{3}$，DE=10，则BC等于（ ）
如图，∠ADE=∠ACB，且$\frac{AD}{AC}$=$\frac{2}{3}$，DE=10，则BC等于（ ）| A． | 12 | B． | 15 | C． | 18 | D． | 20 |
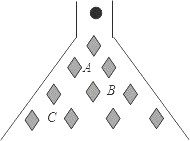如图所示，当以实心小球从入口落下，它在依次碰到每层菱形挡块时，会等可能地向左或向右落下，求小球下落到第三层B位置的概率$\frac{3}{8}$．