题目内容
5．
如图，将△ABC沿BC方向平移4cm得到△DEF，若△ABC的周长为20cm，则四边形ABFD的周长为28cm．
分析 根据平移的基本性质，得出四边形ABFD的周长=AD+AB+BF+DF=4+AB+BC+4+AC即可得出答案．
解答 解：根据题意，将周长为20cm的△ABC沿BC方向平移4cm得到△DEF，
∴AD=CF=4cm，BF=BC+CF，DF=AC；
又∵AB+BC+AC=20cm，
∴四边形ABFD的周长=AD+AB+BF+DF=4+AB+BC+4+AC=28cm．
故答案为28cm．
点评 本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．得到CF=AD，DF=AC是解题的关键．
练习册系列答案
相关题目
20．
如图，已知DE∥FG∥BC，且将△ABC分成面积相等的三部分，若BC=15，则FG的长度是（ ）
如图，已知DE∥FG∥BC，且将△ABC分成面积相等的三部分，若BC=15，则FG的长度是（ ）| A． | 5$\sqrt{6}$ | B． | 10 | C． | 4$\sqrt{3}$ | D． | 7.5 |
10．
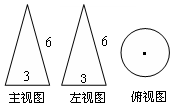一个几何体的三视图如图，其中主视图都是腰长为6、底边长为3的等腰三角形，则这个几何体的侧面展开图的面积为（ ）
一个几何体的三视图如图，其中主视图都是腰长为6、底边长为3的等腰三角形，则这个几何体的侧面展开图的面积为（ ）| A． | 3π | B． | 18π | C． | 8π | D． | 9π |
17．下列事件中，是随机事件的有几个？（ ）
①小明骑车去上学，经过某个十字路口时遇红灯．
②水中捞月
③抛掷一个均匀的骰子，3点朝上．
④367人中至少有2人的生日相同．
⑤如果a，b都是实数，那么 $\sqrt{{a^2}+{b^2}}$＜0
⑥打开电视，它正在播广告．
①小明骑车去上学，经过某个十字路口时遇红灯．
②水中捞月
③抛掷一个均匀的骰子，3点朝上．
④367人中至少有2人的生日相同．
⑤如果a，b都是实数，那么 $\sqrt{{a^2}+{b^2}}$＜0
⑥打开电视，它正在播广告．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
15．顺次连结对角线互相垂直的四边形各边上的中点，得到的新四边形是（ ）
| A． | 矩形 | B． | 正方形 | C． | 菱形 | D． | 平行四边形 |