题目内容
7．
如图，∠ADE=∠ACB，且$\frac{AD}{AC}$=$\frac{2}{3}$，DE=10，则BC等于（ ）| A． | 12 | B． | 15 | C． | 18 | D． | 20 |
分析 先证明△ACB∽△ADE，然后依据相似三角形的性质求解即可．
解答 解：∵∠A=∠A，∠ADE=∠ACB，
∴△ABC∽△ADE．
∴$\frac{DE}{BC}$=$\frac{AD}{AC}$=$\frac{2}{3}$，即$\frac{10}{BC}$=$\frac{2}{3}$，解得：BC=15．
故选：B．
点评 本题主要考查的是相似三角形的性质和判定，证得△ABC∽△ADE是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
17．下列事件中，是随机事件的有几个？（ ）
①小明骑车去上学，经过某个十字路口时遇红灯．
②水中捞月
③抛掷一个均匀的骰子，3点朝上．
④367人中至少有2人的生日相同．
⑤如果a，b都是实数，那么 $\sqrt{{a^2}+{b^2}}$＜0
⑥打开电视，它正在播广告．
①小明骑车去上学，经过某个十字路口时遇红灯．
②水中捞月
③抛掷一个均匀的骰子，3点朝上．
④367人中至少有2人的生日相同．
⑤如果a，b都是实数，那么 $\sqrt{{a^2}+{b^2}}$＜0
⑥打开电视，它正在播广告．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
18．已知平行四边形ABCD中，∠A=100°，则∠C的度数是（ ）
| A． | 100° | B． | 160° | C． | 60° | D． | 80° |
15．顺次连结对角线互相垂直的四边形各边上的中点，得到的新四边形是（ ）
| A． | 矩形 | B． | 正方形 | C． | 菱形 | D． | 平行四边形 |
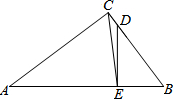如图，在△ABC中，∠ACB=90°，AC=4，BC=3，点D在边BC上，BD=5CD，DE⊥AB，垂足为E．
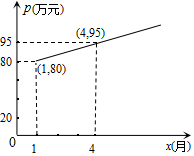在气候对人类生存压力日趋加大的今天，发展低碳经济，全面实现低碳生活成为人们的共识，某企业采用技术革新，节能减排，经分析前5个月二氧化碳排放量y（吨）与月份x（月）之间的函数关系是y=-2x+50．
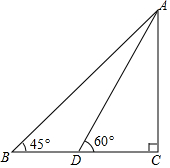如图，某滑雪运动员训练时的斜坡示意图，某次训练拟将难度系数加大，决定将训练的斜坡的倾角由45°升为60°，已知原斜坡AB的长为3$\sqrt{6}$米，点B、D、C在同一水平地面上．若斜坡的正前方能有6米长的空地就能保证安全，已知原斜坡屈的前方有3米长的空地，进行这样的改造是否可行？并说明理由．（参考数据：$\sqrt{3}$=1.732，$\sqrt{6}$=2.449）