题目内容
8.解方程组:$\left\{\begin{array}{l}{\sqrt{3}x-{y}^{2}-3\sqrt{3}=0}\\{2x-\sqrt{3}y-6=0}\end{array}\right.$.分析 先消去一个未知数再解关于另一个未知数的一元二次方程,把求得结果代入一个较简单的方程中即可.
解答 解:$\left\{\begin{array}{l}{\sqrt{3}x-{y}^{2}-3\sqrt{3}=0①}\\{2x-\sqrt{3}y-6=0②}\end{array}\right.$,
由②得,x=$\frac{\sqrt{3}}{2}$y+3③,
把③代入①得,
$\frac{3}{2}$y-y2=0,
解得,y1=0,y2=$\frac{3}{2}$,
当y=0时,x=3,
当y=$\frac{3}{2}$时,x=$\frac{3\sqrt{3}}{4}$+3,
则方程组的解为:$\left\{\begin{array}{l}{{x}_{1}=3}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{3\sqrt{3}}{4}+3}\\{{y}_{2}=\frac{3}{2}}\end{array}\right.$.
点评 本题考查的是二元二次方程组的解法,掌握代入消元法是解题的关键,先消去一个未知数再解关于另一个未知数的一元二次方程,把求得结果代入一个较简单的方程中求出未知数.

练习册系列答案
相关题目
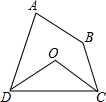 如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,求∠COD的度数.
如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,求∠COD的度数.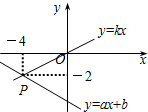 如图,已知一次函数y=ax+b(a≠0)和y=kx(k≠0)的图象交于点P(-4,-2),则不等式ax+b>kx的解是x<-4.
如图,已知一次函数y=ax+b(a≠0)和y=kx(k≠0)的图象交于点P(-4,-2),则不等式ax+b>kx的解是x<-4.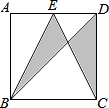 如图,正方形ABCD的边长为3,E为AD的中点,连接BE、BD、CE,则图中阴影部分的面积是3.
如图,正方形ABCD的边长为3,E为AD的中点,连接BE、BD、CE,则图中阴影部分的面积是3.