题目内容
4.抛物线y=x2-2x+c经过点(2,1).(1)求抛物线的顶点坐标;
(2)将抛物线y=x2-2x+c沿y轴向下平移后,所得新抛物线与x轴交于A、B两点,如果AB=2,求新抛物线的表达式.
分析 (1)把(2,1)代入y=x2-2x+c中求出c的值即可得到抛物线解析式,然后配成顶点式得到顶点坐标;
(2)先确定抛物线y=x2-2x+1的对称轴,再利用抛物线的对称性得到A(0,0),B(2,0),然后利用交点式可写出新抛物线的表达式.
解答 解:(1)把(2,1)代入y=x2-2x+c得4-4+c=1,解得c=1,
所以抛物线解析式为y=x2-2x+1,
y=(x-1)2,
所以抛物线顶点坐标为(1,0);
(2)y=x2-2x+1=(x-1)2,抛物线的对称轴为直线x=1,
而新抛物线与x轴交于A、B两点,AB=2,
所以A(0,0),B(2,0),
所以新抛物线的解析式为y=x(x-2),即y=x2-2x.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列说法正确的是( )
| A. | -1000是10-6的算术平方根 | B. | 6的平方根是$\sqrt{6}$ | ||
| C. | $\sqrt{3}$是3的平方根 | D. | -n没有平方根 |
9.下列各式从左到右的变形正确的是( )
| A. | $\frac{0.2a+b}{a+0.2b}=\frac{2a+b}{a+2b}$ | B. | $\frac{a+b}{a-b}=-\frac{a-b}{a+b}$ | ||
| C. | $\frac{20x+y}{50x-y}=\frac{2+y}{5x-y}$ | D. | $-\frac{x+1}{x-y}=\frac{x+1}{y-x}$ |
16.某汽车生产厂家经过市场调研,决定从明年开始对A、B两种品牌的汽车实施“限产压库”,要求这两种品牌的汽车全年共新增产量200辆,甲、乙两种品牌的汽车产值如表所示:
(1)若全年两种品牌新增汽车的总产值为1260万元,那么该公司如何安排A、B两种品牌汽车的生产量?
(2)若全年总产值为P,且1100<P<1200,那么该公司安排生产A种品牌汽车最多多少辆?
| 汽车品牌 | 每辆汽车的产值 |
| A | 4.5万元 |
| B | 7.5万元 |
(2)若全年总产值为P,且1100<P<1200,那么该公司安排生产A种品牌汽车最多多少辆?
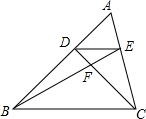 如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$.
如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$.