题目内容
20.下列计算正确的是( )| A. | $\sqrt{4}-\sqrt{2}=\sqrt{2}$ | B. | $\sqrt{8}=4\sqrt{2}$ | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ |
分析 根据二次根式的加减法对A、C进行判断;根据二次根式的性质对B进行判断;根据二次根式的乘法法则对D进行判断.
解答 解:A、原式=2-$\sqrt{2}$,所以A选项错误;
B、原式=2$\sqrt{2}$,所以B选项错误;
C、$\sqrt{2}$与$\sqrt{3}$不能合并,所以C选项错误;
D、原式=$\sqrt{2×3}$=$\sqrt{6}$,所以D选项正确.
故选D.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
10.直线y=kx+b与直线y=2x+2014平行,且与y轴交于点M(0,4),则其函数关系式是( )
| A. | y=-2x-4 | B. | y=2x+4 | C. | y=-2x+4 | D. | y=2x-4 |
11.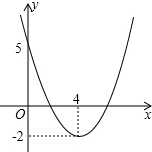 二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
 二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )| A. | m≥-2 | B. | m≥5 | C. | m≥0 | D. | m>4 |
8.已知二次函数y=2(x-3)2+1.下列说法:
①其图象的开口向下;
②其图象的对称轴为直线x=-3;
③其图象顶点坐标为(3,-1);
④当x<3时,y随x的增大而减小.
其中正确的说法有( )
①其图象的开口向下;
②其图象的对称轴为直线x=-3;
③其图象顶点坐标为(3,-1);
④当x<3时,y随x的增大而减小.
其中正确的说法有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.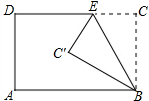 如图所示,将矩形ABCD沿BE折叠,若∠ABC′=30°,则∠BEC′等于( )
如图所示,将矩形ABCD沿BE折叠,若∠ABC′=30°,则∠BEC′等于( )
 如图所示,将矩形ABCD沿BE折叠,若∠ABC′=30°,则∠BEC′等于( )
如图所示,将矩形ABCD沿BE折叠,若∠ABC′=30°,则∠BEC′等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
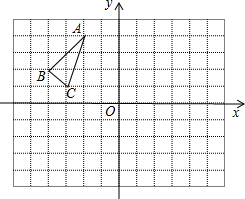 △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图: