题目内容
9.抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点.(1)当a=1,b=3,c=2时,求A、B两点及抛物线的顶点的坐标;
(2)若a:b:c=1:3:2时,A、B两点的坐标及抛物线的顶点的坐标是否发生变化?若不变,求出坐标,若变化,说明理由.
(3)当b=3,c=2时,若抛物线y=ax2+bx+c与x轴的交点中有且仅有一个在原点和点(1,0)之间(不含这两个点),则a的取值范围是a<-5.
分析 (1)把a=1,b=3,c=2代入抛物线解析式,令y=0,求出A、B两点坐标,再把抛物线一般式化为顶点坐标式,即可求出顶点坐标;
(2)根据a:b:c=1:3:2,设a=k,b=3k,c=2k,令y=kx2+3kx+2k=k(x2+3x+2)=0,即可求出A、B两点坐标,发现顶点坐标发生变化;
(3)由b2-4ac>0,可知a<$\frac{9}{8}$,分析0<a<$\frac{9}{8}$,a<0,由与x轴的交点中有且仅有一个在原点和点(1,0)之间(不含这两个点),可得到a的取值范围.
解答 解:(1)当a=1,b=3,c=2时,y=x2+3x+2,
令y=x2+3x+2=0,
解得x=-1或x=-2,
即A、B两点为(-1,0)、(-2,0),
∵y=x2+3x+2=(x+$\frac{3}{2}$)2-$\frac{1}{4}$,
∴抛物线顶点坐标为(-$\frac{3}{2}$,-$\frac{1}{4}$);
(2)若a:b:c=1:3:2,设a=k,b=3k,c=2k,
则y=kx2+3kx+2k=k(x2+3x+2)
令y=kx2+3kx+2k=k(x2+3x+2)=0,
解得x=-1或x=-2,
即A、B两点为(-1,0)、(-2,0),
y=k(x2+3x+2)=k[(x+$\frac{3}{2}$)2-$\frac{1}{4}$],
∴抛物线顶点坐标为(-$\frac{3}{2}$,-$\frac{1}{4}$k);
∴A、B两点的坐标不发生变化,顶点坐标发生变化;
(3)a<-5,
当b=3,c=2时,y=ax2+3x+2,
∵b2-4ac>0,
∴9-8a>0,
解得:a<$\frac{9}{8}$,
∵抛物线y=ax2+bx+c与x轴的交点中有且仅有一个在原点和点(1,0)之间(不含这两个点),
若0<a<$\frac{9}{8}$,抛物线与x轴交点均在x轴的负半轴上,与题意不符,
若a<0,当x=1时,y<0,即a+3+2<0,
∴a<-5.
故答案为:a<-5.
点评 本题主要考查了抛物线与x轴交点,解答本题的关键是熟练掌握把抛物线一般式化成顶点坐标式,明确二次函数与一元二次方程的关系.

| A. | $\sqrt{4}-\sqrt{2}=\sqrt{2}$ | B. | $\sqrt{8}=4\sqrt{2}$ | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ |
| A. | 互为邻补角的两个角一定不相等 | B. | 互为对顶角的两个角有可能不相等 | ||
| C. | 互为内错角的两个角一定相等 | D. | 互为同旁内角的两个角有可能相等 |
| 姓名 | A | B | C | D | E | F |
| 身高 | 165 | 169 | 167 | 164 | 171 | 172 |
| 身高与班级平均身高的差值 | -2 | +2 | 0 | -3 | +4 | +5 |
(2)他们的最高与最矮相差多少?
(3)他们的平均身高是多少?
 如图,△ABC为等边三角形,D为BA延长线上一点,E为线段BC上一点,连接DE、DC,且∠BDE=∠ACD,求证:AD=BE.
如图,△ABC为等边三角形,D为BA延长线上一点,E为线段BC上一点,连接DE、DC,且∠BDE=∠ACD,求证:AD=BE.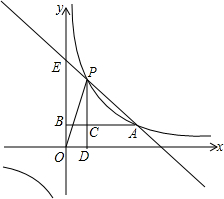 双曲线$y=\frac{k}{x}(k>0)$,点A(m,n)(m>0)在此双曲线上,过点A作AB垂直y轴交y轴于点B,点C在线段AB上,过点C作直线CD⊥x轴于点D,交此双曲线于点P.直线PA交y轴于点E.
双曲线$y=\frac{k}{x}(k>0)$,点A(m,n)(m>0)在此双曲线上,过点A作AB垂直y轴交y轴于点B,点C在线段AB上,过点C作直线CD⊥x轴于点D,交此双曲线于点P.直线PA交y轴于点E. 如图,已知四边形ABCD,平移四边形ABCD,使点B经平移后落在点D处,请用作图的方法作出经这一平移后所得的图形.
如图,已知四边形ABCD,平移四边形ABCD,使点B经平移后落在点D处,请用作图的方法作出经这一平移后所得的图形.