题目内容
15.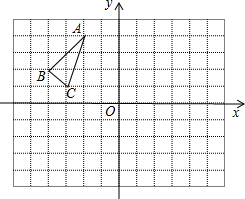 △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点C顺时针旋转90°得到△A2B2C.
分析 ①根据关于原点中心对称的点的坐标特征,分别描出点A、B、C的对应点A1、B1、C1,即可得到△A1B1C1;
②利用网格特点,根据旋转的性质画出点A、B旋转后的对应点A2、B2,即可得到△A2B2C.
解答 解:①如图,△A1B1C1为所作;
②如图,△A2B2C为所作.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
10.教材第25页有这样一段话:“一般地,如果二次函数y=ax2+bx+c的图象与x轴(注:x轴即直线y=0)有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”反之,利用函数的图象判断方程x2-x-6=$\frac{1}{x}$实数根的情况是( )
| A. | 有三个实数根 | B. | 有两个实数根 | C. | 有一个实数根 | D. | 无实数根 |
20.下列计算正确的是( )
| A. | $\sqrt{4}-\sqrt{2}=\sqrt{2}$ | B. | $\sqrt{8}=4\sqrt{2}$ | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ |
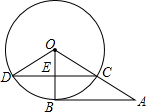 如图,A为⊙O外一点,AB切⊙O于点B,AO交⊙O于C,CD⊥OB于E,交⊙O于点D,连接OD,若AB=8,AC=4.
如图,A为⊙O外一点,AB切⊙O于点B,AO交⊙O于C,CD⊥OB于E,交⊙O于点D,连接OD,若AB=8,AC=4. 如图,已知四边形ABCD,平移四边形ABCD,使点B经平移后落在点D处,请用作图的方法作出经这一平移后所得的图形.
如图,已知四边形ABCD,平移四边形ABCD,使点B经平移后落在点D处,请用作图的方法作出经这一平移后所得的图形.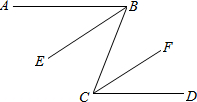 如图,已知AB∥CD,BE、CF分别平分∠ABC和∠BCD,探索BE与CF的位置关系,并说明理由.
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠BCD,探索BE与CF的位置关系,并说明理由.