题目内容
是否存在这样一个正整数,当它加上100时是一个完全平方数,当它加上129时是另一个完全平方数?若存在,请求出这个正整数;若不存在,请说明理由.
考点:完全平方数
专题:
分析:利用分解因式求不定方程的整数解,再求m的值,进而得出答案.
解答:解:假设存在这样的正整数m,由题意得:
m+100=x2①;m+129=y2②,
②-①得y2-x2=29.所以(y+x)(y-x)=29×1.
只有当x+y=29,y-x=1时,成立,即
,
解得:
,
所以m=x2-100=142-100=196-100=96,
∴存在正整数96,当它加上100时是一个完全平方数,当它加上129时是另一个完全平方数.
m+100=x2①;m+129=y2②,
②-①得y2-x2=29.所以(y+x)(y-x)=29×1.
只有当x+y=29,y-x=1时,成立,即
|
解得:
|
所以m=x2-100=142-100=196-100=96,
∴存在正整数96,当它加上100时是一个完全平方数,当它加上129时是另一个完全平方数.
点评:此题主要考查了运用公式法因式分解以及二元一次方程组的解法,得出x+y=29,y-x=1是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
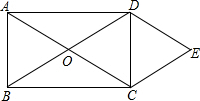 如图,矩形ABCD中,对角线AC、BD交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD中,对角线AC、BD交于点O,DE∥AC,CE∥BD. 如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点F,AD与CE相交于点G,且CG=AB.
如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点F,AD与CE相交于点G,且CG=AB.